Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 192
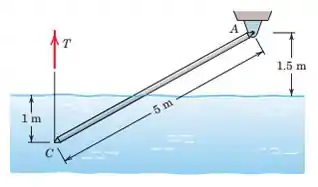
O mastro uniforme de 62 kg de 150 mm de diâmetro é articulada em A, e sua extremidade inferior está imersa em agua. Determine a tensão T no cabo vertical
necessário para manter C a uma profundidade de 1 m.
Passo 1
E ai gurizada tudo belezinha???
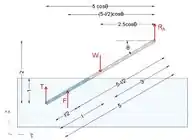
A seguir, isolaremos e desenharemos o diagrama de corpo livre da haste com seu peso, tensão do cabo, força de reação em A e força de flutuabilidade atuando sobre ele.
O peso do mastro é:
Passo 2
Observe que a força de flutuabilidade atua no contróide da parte inundada da haste. Usando proporções, podemos determinar o comprimento da parte inundada.
Como o diâmetro do poste é , o volume da parte inundada é:
A força de empuxo é igual ao produto da densidade, volume e gravidade da água.
Substitua V e g por seus valores e por 1000Kg/m³ na expressão para F.
Passo 3
Equacionando a soma dos momentos sobre o ponto A a zero, podemos determinar a tensão T.
Divida os dois lados da equação por
Substitua F, W e por seus valores.
A partir daqui, podemos expressar T como: