Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 193

Uma extremidade de um pólo uniforme de comprimento L e densidade ρ ´ é fixado em C ao fundo de um tanque de líquido de densidade ρ   e profundidade h. Para as condições ρ ´ < ρ       e, encontre o ângulo assumido pelo pólo.

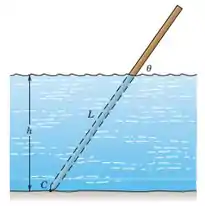
Passo 1

E ai gurizada tudo belezinha???

Para isso, precisamos determinar o ângulo θ na imagem:

Primeiro vamos definir o W.

W = ρ ´ g L A

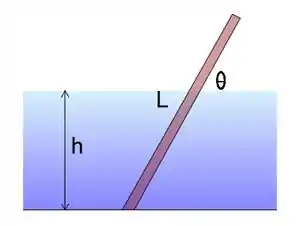
Passo 2

E aqui temos toda a força de flutuabilidade B.

B = ρ g V

V = A L

V = A   A   h sin ⁡ θ

B = ρ g   A   h sin ⁡ θ

Passo 3

E finalmente vamos definir o ângulo .... através do equilíbrio.

∑ M C = 0

B × b - - W × ω - = 0

ρ g A   h sin ⁡ θ × h 2 sin ⁡ θ cos ⁡ θ - ρ ´ g   L A × l 2  cos ⁡ θ = 0

ρ g A   h sin ⁡ θ × h 2 sin ⁡ θ cos ⁡ θ - ρ ´ g   L A × l 2  cos ⁡ θ

h sin ⁡ θ 2   ρ = L ² ρ ´

h L  sin ⁡ θ 2 = ρ ´ ρ

h L sin ⁡ θ = ρ ´ ρ ´

sin ⁡ θ = h L   ρ ´ ρ ´

Resposta

a) θ = s i n - 1 h L   ρ ´ ρ  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície e o volume do sólido girando-se a área sombreada 360° em torno do eixo z .
O reservatório de água possui teto em formato paraboloide. Se um litro de tinta pode cobrir 3 m³ do tanque, determine o número de litros necessários para cobrir o teto.
Metade da seção transversal do flange de aço aparece na figura. Existem seis furos de parafuso com 10m m de diâmetro em torno de sua borda. Determine sua massa. A densidade do aço é 7,85M g / m ³ ³ .
Uma roda de aço tem diâmetro de 840m m e uma seção transversal conforme a figura. Determine a massa total da roda se r=5M g / m ³ ³ .
Um canal de água doce com 10 pés de largura (normal para o plano do papel) é bloqueado em sua extremidade por uma barreira retangular, mostrada na seção ABD. As escoras de suporte BC são espaçadas a c