Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 92

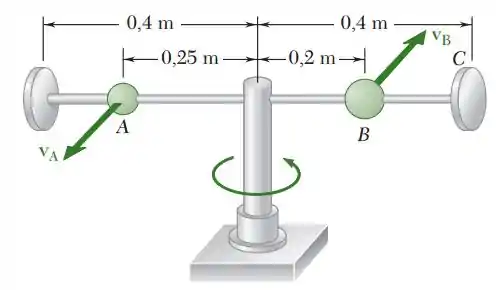
Uma bola A de 200 g e uma bola B de 400 g são montadas em umabarra horizontal que gira livremente sobre um eixo vertical. As bolassão mantidas nas posições mostradas na figura por pinos. O pino quesegura B é repentinamente removido e a bola se move para a posiçãoC enquanto a barra gira. Desprezando o atrito e a massa da barra esabendo que a velocidade escalar inicial de A é v A = 2,5   m/s, determine (a) os componentes radial e transversal da aceleração da bola Bimediatamente após o pino ser retirado, (b) a aceleração da bola B relativa à barra nesse instante, (c) a velocidade escalar da bola A depoisda bola B ter atingido o batente em C.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine (a) os componentes radial e transversal da aceleração da bola Bimediatamente após o pino ser retirado, (b) a aceleração da bola B relativa à barra nesse instante, (c) a velocidade escalar da bola A depoisda bola B ter atingido o batente em C.

Seja r e θ coordenadas polares com a origem situada no eixo.

Restrição da haste:

θ_B= θ_A+π radiandos; θ ̇_B= (θ_A ) ̇=θ ̇; (θ_B ) ̈= (θ_A ) ̈=θ ̈.

(a) Componentes de aceleração:

Esboce os diagramas do corpo das bolas mostrando os componentes radiais e transversais das forças que atuam sobre elas. Devido ao deslizamento sem atrito de B ao longo da haste,

( F B ) r = 0 .

Componente radial de aceleração de B.

F r = m B ( a B ) r : ( a B ) r = 0

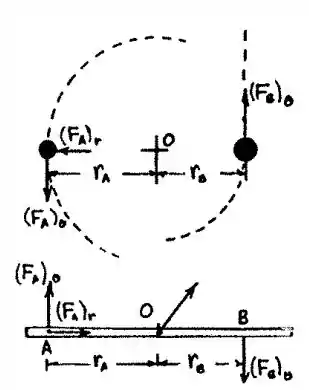
Componentes transversais de aceleração.

( a A ) θ = r A θ ¨ + 2 r A ˙   θ ˙ = r a θ ¨

( a A ) θ = r B θ ¨ + 2 r B ˙   θ ˙ (1)

Uma vez que a barra não tem massa, ela deve estar em equilíbrio. Desenhe seu diagrama de corpo livre, aplicando a terceira lei de Newton.

+ ) ∑ M 0 = 0 :               r A ( F A ) θ + r B ( F B ) θ = r A m A ( a A ) θ + r B m B ( a B ) θ = 0

r A m A r A θ ¨ + r B m B r B θ ¨ + 2 r B ˙ θ ˙ = 0

θ ¨ = - 2   r B r B ˙   θ ˙ ˙ m A r A m B r B ²

Em: t = 0 , r B ˙ = 0 de modo a θ ¨ = 0

Frente Eq. (1)

Passo 2

(b)Aceleração de B em relação a haste:

Em: t = 0 ( a A ) θ = 2.5   m / s ,   θ ˙ = ( v A ) θ r A = 2.5 0.25 = 10   r a d / s

r B ¨ - r B θ 2 ˙ = ( a B ) r = 0

r B ¨ - r B θ 2 ˙ = 0.2 10 2 = 20   m / s ²

Passo 3

(C) Velocidade de A:

Substituindo d d t ( m 2 θ ˙ ) para r F θ em cada termo de equação de momento da:

d d t   ( m A r ² A θ ˙ ) +   d d t   ( m B r 2 B θ ˙ ) = 0

Integrado com respeito ao tempo,

m A r 2 A θ ˙ +   m B r ² B θ ˙ = ( m A r 2 A θ ˙ ) 0 + ( m B r ² B θ ˙ ) 0

Aplicando-se ao estado de localização com a bola B movida para a parada em C.

( m A r 2 A +   m B r ² C )   θ ∫ ˙ = [ m A r 2 A +   m B r B ) 0 2 θ 0 ˙

θ ∫ ˙ = m A r 2 A +   m B r B 2 m A r 2 A +   m B r C 2 = 0.2 0.25 2 + ( 0.4 ) ( 0.2 ) ² 0.2 0.25 2 + ( 0.4 ) ( 0.4 ) ²   = 3.7255   r a d / s

( v A ) ∫ = r A θ ∫ ˙ = ( 0.25 ) ( 3.7255 ) = 0.93137   m / s

Resposta

a)   ( a B ) θ = 0

b) r B ¨ = 20.0   m / s ²

c) ( v A ) ∫ = 0.931   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco A pode se mover sem atrito na fenda como mostrado nafigura e sobre ele atuar uma força vertical periódica de intensidade P = P ms e nω ƒ t ƒ , onde ω ƒ = ƒ 2 rad /s e P m = 20 N. Uma mola de c
Um pequeno reboque e sua carga têm uma massa total de 250 kg.O reboque é suportado por duas molas, cada uma de constante10 kN/m, e puxado sobre uma estrada cuja superfície pode ser aproximada por uma
Desenhe o análogo elétrico do sistema mecânico mostrado. (Dica: desenhe os loops correspondentes aos corpos livres m e A.)
Expresse em termos de L, C e E a faixa de valores da resistência R para a qual as oscilações ocorrerão no circuito mostrado quando a chave S for fechada.
Um elemento de máquina de 500 kg é suportado por duas molas, cada uma de constante 50 kN/m. Uma força periódica de 150 N de amplitude é aplicada ao elemento com uma frequência de 2,8 Hz. Sabendo que o