Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 153

Uma bola é chutada com velocidade escalar inicial v A = 8   m / s a um ângulo θ A = 40 ° com a horizontal. Encontre a equação da trajetória, y = f ( x ) , e, em seguida, determine as componentes normal e tangencial da sua desaceleração quando t = 0,25 s.

Passo 1

O enunciado nos diz que :

Velocidade escalar em A : v = 8 m/s;

Ângulo com a horizontal: θ = 40 ° ;

Devemos determinar a equação da trajetória e as componentes normal e tangencial da aceleração quando t = 0,25 s.

Passo 2

Primeiramente, vamos analisar o movimento na horizontal.

A componente da velocidade na horizontal é

v x = 8 cos ⁡ 40 ° = 6,128   m / s

O deslocamento inicial é s 0 x = 0 e o deslocamento final será de s x = x .

Logo,

s x = s 0 x + v x t

x = 0 + 6,128 t

Passo 3

Em seguida, vamos analisar o movimento na vertical.

A componente da velocidade na vertical é

v y = 8 sen ⁡ 40 ° = 5,142   m / s

O deslocamento inicial é s 0 y = 0 e o deslocamento final será de s y = y .

Logo,

s y = s 0 y + v y t + 1 2 a t 2

y = 0 + 5,142 t + 1 2 - 9,81 t 2

A aceleração da gravidade é negativa pois age no sentido contrário ao deslocamento em y .

Passo 4

Agora vamos unir as equações obtidas anteriormente para obter y = f ( x ) .

Temos

x = 6,128 t

Logo,

t = x 6,128

Substituindo em y , obtemos

y = 5,142 x 6,128 + 1 2 - 9,81 x 6,128 2

y = 0,8 39 x - 0,131 x 2

Passo 5

Em seguida, vamos determinar as componentes normal e tangencial da desaceleração da bola quando t = 0,25 s.

A componente normal da aceleração está sempre direcionada para o centro da curvatura da trajetória, ou seja, ao longo do eixo positivo normal n . Este eixo é perpendicular à tangente da trajetória.

A tangente da trajetória é dada por

d y d x = 0,839 - 0,262 x

E

α = tan - 1 ⁡ d y d x

Onde o ângulo α é o ângulo que a tangente faz com o eixo x .

Em t = 0,25 s, temos que

x = 6,128 t = 1,532   m

d y d x = 0,839 - 0,262 x = 0,4389

α = tan - 1 ⁡ d y d x = 23,7 °

Para uma melhor visualização, desenhamos como os eixos estão relacionados:

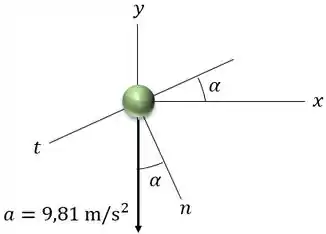
Portanto, temos que, em t = 0,25 s,

a n = a cos ⁡ α = 9,81 cos ⁡ 23,7   ° = 3,94   m / s 2

a t = a sen ⁡ α = 9,81 sen ⁡ 23,7   ° = 8,98   m / s 2

Resposta

y = 0,839 x - 0,131 x 2

a n = 3,94   m / s 2

a t = 8,98   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se a sua posição é θ ˙ = 3 t 2 rad/s, onde t é dado em segundos, determine as instensidades da velocidade e aceleração da part
2/112 ) Um carro faz uma curva de curvatura constante entre A e B com uma velocidade também constante de 45 quilômetros por hora . Se um acelerômetro foi montado no carro , qual módulo da aceleração e
2/110) Considere o eixo polar da terra como fixo no espaço e calcule o módulo da aceleração a de um ponto P sobre a superfície da terra a uma latitude de 40 ° norte . O diâmetro médio da terra é 12742
2/109 ) A figura mostra duas trajetórias possíveis para passar por uma curva sem inclinação lateral em uma parte horizontal de uma pista de corrida . A trajetória A-Asegue a linha central da estrada e
2/114) Uma nave espacial S está em órbita de júpiter em uma trajetória circular de 1000k m acima dasuperfície com umavelocidade constante . Utilizando a lei gravitacional , calcule omódulo v de sua ve