Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 94
A tábua de 25 kg está suspensa pelas cordas em C e D. Se essas cordas estão submetidas a forças constantes de 150 N e 225 N, respectivamente, determine a aceleração inicial do centro da tábua e sua aceleração angular. Suponha que a tábua seja uma placa fina. Despreze a massa das polias em E e F.
Passo 1
Começaremos o exercício calculando o momento de inércia da tábua em relação ao seu centro de massa:
Passo 2
Agora iremos aplicar o somatório de forças na direção y com o auxílio da figura a seguir:
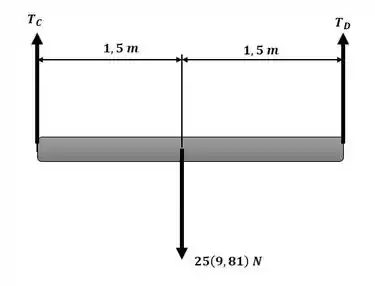
Passo 3
Agora aplicando o somatório de momento com relação ao centro de massa da tábua, ainda com o auxílio da figura do passo 2, temos:
Resposta
Exercícios de Livros Relacionados
A barra uniforme tem uma massa de 15 kg. Determine as componentes verticais e horizontais da reação no pino O, e a aceleração angular da barra logo após a barra ser cortada.
O hemisfério é formado girando-se a área sombreada em torno do eixo y . Determine o mometo de inércia I y e expresse o resultado em termos da massa total m do hemisfério. O material tem uma densidade
Determine o momento de inércia I y para a barra fina. A densidade da barra ρ e a área de seção transversal A são constante. Expresse o resultado em termos da massa total m da barra.
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo centro de massa G . O material tem um peso específico de γ = 15KN/m3.
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo ponto O . O material tem um peso específico de γ = 15KN/m3.