A barra está presa por um pino em e é sustentada por duas hastes de alumínio, cada uma com diâmetro de e módulo de elasticidade . Considerando que a barra é rígida e inicialmente vertical, determine a força em cada haste quando for aplicada uma força de .
Passo 1
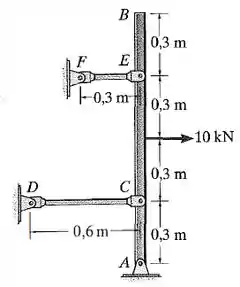
Falaaa! Uma barra vertical rígida está presa a duas hastes em e , e a um pino em .
Características das hastes e :
- Alumínio: .
- Diâmetro: .
- Comprimento inicial: e
Uma força horizontal de puxa a barra para a direita bem no meio dela. A barra rígida vai girar ao redor do pino em .
Queremos saber a força desenvolvida na haste e na haste . Bora!
Passo 2
Pra achar forças, começamos com diagrama de corpo livre. Só as reações horizontais nos interessam aqui.
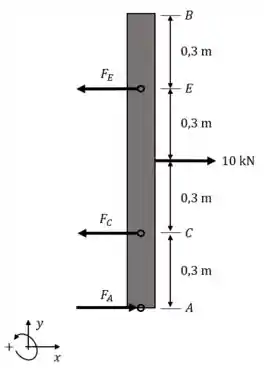
Vamos fazer o equilíbrio de momentos no ponto , assim a força não contribui.
Se a gente dividir geral por 0,3, vamos ter:
Precisamos de outra equação que relacione apenas essas forças. Vejamos a condição de compatibilidade.
Passo 3
A barra vai girar ao redor do pino em . Como ela é rígida, ela não se deforma. Mas as hastes vão se deformar. Elas se alongam.
Vamos ver como os deslocamentos das hastes se relacionam. A barra é a linha preta na figura.
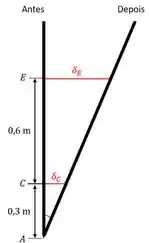
A geometria do alongamento das hastes é esse porque nossa barra precisa sempre ficar reta.
Há dois triângulos nessa figura com um ângulo em comum. Podemos usar semelhança de triângulos e escrever:
Lembrando da fórmulinha do deslocamento para carga axial:
Ficamos com essa relação carga-deslocamento:
Substituímos os valores de para achar:
Passo 4
Usamos em para obter
Prontinho!
Resposta
Força na haste : .
Força na haste :.