Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 103
Uma bola de futebol americano deve ser chutada sobre o poste do gol que fica a 4,5 m de altura. Se a sua velocidade escalar inicial é , determine se ela consegue ultrapassar o poste do gol, e, se conseguir, qual o valor de .
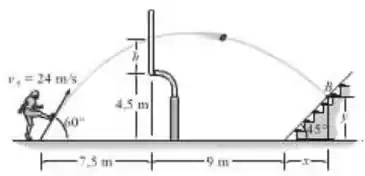
Passo 1
Temos um problema de lançamento oblíquo! A bola possuirá componentes e da velocidade. Na direção , temos a ação da gravidade. É por sua causa que a bola possui uma trajetória arqueada, subindo e posteriormente descendo. Já na direção do eixo ela possui velocidade constante.
Precisamos determinar inicialmente o tempo necessário para que a bola percorra a distância de 7,5 m na direção do eixo , e assim, chegará na posição do poste. Com este valor do tempo, utilizaremos na equação da cinemática na direção do eixo , a fim de descobrir a posição da bola. A partir do valor que encontrarmos saberemos se a bola conseguirá ultrapassar ou não o poste do gol.
Passo 2
Vamos começar determinando o tempo . Na direção do eixo temos:
Portanto, a bola necessita de para atingir a posição do poste.
Passo 3
Agora, vamos analisar na direção qual a posição da partícula após do seu lançamento. Desta forma, temos:
Portanto, como , a bola consegue ultrapassar o poste do gol. Além disto, o valor da distância é:
Resposta
A bola realmente consegue ultrapassar o poste do gol.