Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 79
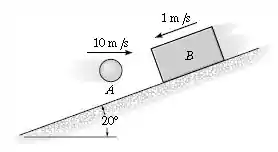
A bola de é lançada de modo a se mover horizontalmente a quando atinge o bloco de , que está descendo o plano inclinado a . Se o coeficiente de restituição entre a bola e o bloco é , determine as velocidades da bola e do bloco logo após o impacto. Além disso, que distância desliza plano acima antes de parar momentaneamente? O coeficiente de atrito cinético entre o bloco e o plano .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom galera... para determinar as velocidades após o impacto, temos que aplicar a conservação de movimento linear:
Podemos aplicar o conceito de restituição para encontrar outra equação que nos ajude a resolver o sistema:
Podemos somar as duas equações que achamos:
Logo:
Passo 2
Temos as componentes em das velocidades dos nossos corpos, agora vamos encontrar as componentes em . Sabemos que o bloco B, não terá componente da velocidade em , pois ele tende a seguir o a rampa que consideramos como a nossa componente . Portanto:
Já em , temos que investigar o que acontece em . Vamos aplicar a conservação de quantidade de movimento para o eixo :
Portanto, a magnitude da velocidade de após o impacto, será:
Passo 3
A questão também nos pergunta que distância desliza plano acima antes de parar momentaneamente.
Bom... Para descobrir quanto anda para cima na rampa, após o impacto, antes de parar e começar a descer, podemos aplicar a conservação de energia. Mas primeiro vamos avaliar o diagrama de corpo livre:
Para saber a força de atrito, precisamos descobrir o valor da normal . O somatório das forças em é:
Agora que sabemos o valor da força normal , podemos aplicar a conservação de energia: