Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 193
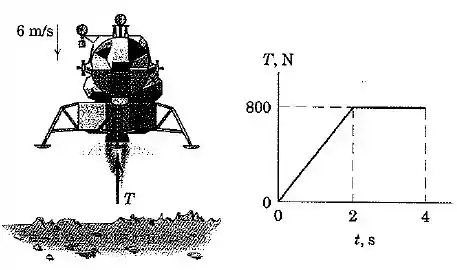
O módulo de aterrissagem lunar de está descendo na superfície da Lua com uma velocidade de quando seu retromotor é acionado. Se o motor produz um empuxo por que varia com o tempo como mostrado e em seguida desliga, calcule a velocidade do módulo de aterrissagem quando , supondo que ele ainda não aterrisou. A aceleração gravitacional na superfície da Lua é .
Passo 1
Vamos aplicar o teorema do impulso na direção vertical:
Isso quer dizer que se integrarmos todas as forças em relação ao tempo nos segundos de movimento, vamos encontrar a variação do momento na direção em questão.
No nosso caso temos duas forças agindo em :
E estamos considerando o sentido positivo como sendo vertical para baixo.
Passo 2
A primeira integral pode ser calculada assim:
E a segunda é simplesmente a área do gráfico que foi dado no enunciado:
Lembrando que a força se anula quando , então não precisamos nos preocupar com isso.
Agora voltando na nossa equação de cima:
Passo 3
Agora podemos substituir os valores numéricos para achar a velocidade final:
Resposta
A velocidade do módulo quando é .