Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 65
A barra fina AB de 12,5 kg está fixada à mola BC, que tem um comprimento não deformado de 1,2 m. Se a barra é liberada do repouso quando = 30°, determine sua velocidade angular no instante em que a mola se torna não deformada.
Passo 1
Iremos considerar a aceleração da gravidade
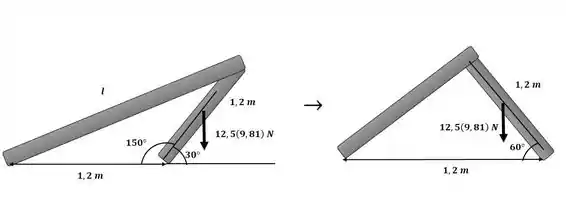
Para poder aplicar a equação da conservação da energia mecânica e determinar a velocidade angular, devemos primeiro encontrar o comprimento da mola deformada. Faremos isso usando a lei dos cossenos e com o auxílio da figura a seguir, que mostra a condição final e inicial do sistema:
Passo 2
Através da análise da figura, temos o triângulo ABC. Para = 30°, o ângulo BÂC = 150°, dessa forma, a lei dos cossenos que é dada por:
Assume a seguinte forma:
Passo 3
Com isso, podemos agora aplicar a equação da conservação da energia mecânica para encontrar a velocidade angular da barra AB:
Observe que o formato é bem parecido com o do problema 18.64, atentar para a diferença no primeiro termo da energia potencial (+), que tem sua localização alterada, da mesma forma e o último termo, que diz respeito a energia final de deformação da mola, como nesse caso a mola estará na condição não deformada, a energia é zero.
Resolvendo a equação para :