Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 17

A bola de 5 kg é lançada na pista com um efeito de giro para trás ω 0 = 10   r a d / s , e a velocidade de seu centro de massa O é v 0 = 5   m / s . Determine o tempo para a bola parar de girar para trás e a velocidade de seu centro de massa nesse instante. O coeficiente de atrito cinético entre a bola e a pista é μ k = 0,08 .

Passo 1

Para resolver esse exercício, iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Sabendo que existe força de atrito cinético entre a bola e a pista, e ela pode ser escrita como:

F a = μ k N = 0,08 N

Vamos encontrar também o momento de inércia da bola, pois esse valor será usado quando aplicarmos o princípio de impulso e momento, sendo assim:

I O = 2 5 m r 2 = 2 5 5 0,1 2

I O = 0,02   k g . m 2

Passo 2

Agora podemos aplicar o princípio do impulso e da quantidade de movimento linear na direção y com o auxílio da imagem a seguir para descobrir o valor da força normal N:

+ ↑       m [ v O y ] 1 + ∑ ∫ t 1 t 2 F y d t = m [ v O y ] 2

0 + N t - 5 9,81 t = 0

N = 49,05   N

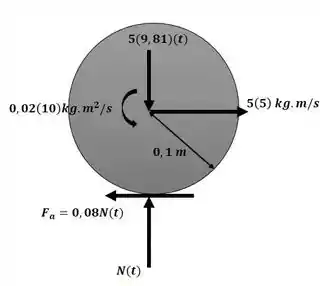
Agora podemos aplicar o princípio do impulso e momento angular para descobrir a velocidade final do centro de massa da bola:

↺ +   H A 1 + ∑ ∫ t 1 t 2 M A d t = H A 2

0,02 10 - 5 5 0,1 + 0 = - 5 v O 2 ( 0,1 )

v O 2 = 4,6   m / s

Passo 3

Agora podemos aplicar o princípio do impulso e momento linear na direção x para descobrir o tempo para a bola parar de girar para trás, sendo assim:

+ →     m [ v O x ] 1 + ∑ ∫ t 1 t 2 F x d t = m [ v O x ] 2

5 5 - 0,08 49,05 t = 5 4,6

t = 0,51   s

Resposta

t = 0,51   s

v O 2 = 4,6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma massa plástica D, de 2 kg, acerta a prancha uniforme ABC, de 10 kg, com uma velocidade de 10 m/s. Se a massa plástica permanece fixada à prancha, determine o ângulo máximo de oscilação antes que a
A bala de 30g tem uma velocidade horizontal de 500m / s quando atinge a barra esbelta O A de 10k g , que está suspensa a partir do ponto O e está inicialmente em repouso. Calcule a velocidade angular
A bala 28g tem uma velocidade horizontal de 500m / s quando atinge o pêndulo composto de 25k g , que tem um raio de giração k o = 925m m . Se a distância h = 1075m m , calcule a velocidade angular ω d
O disco circular uniforme com 200m m de raio tem uma massa de 25kg e está montado sobre a barra giratória O A em trÊs formas diferentes. Em cada caso a barra gira em torno de seu eixo vertical em O co
O momento de atrito M que atua sobre o disco de uma turbina que gira e sobre seu eixo é dado por M = k ω ² ² onde ω é a velocidade angular da turbina. Se a fonte de energia é cortada enquanto a turbin