Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 5
Uma rigidez de e não está deformando quando o bloco de está em . Determine a aceleração do bloco quando . A superfície de contato entre obloco e o plano é lisa.
Passo 1
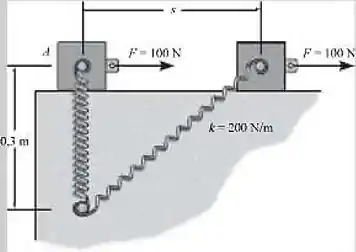
O primeiro passo para o desenvolvimento do problema é saber o quanto a mola de rigidez deformou. Na posição , o comprimento inicial da mola é igual a m e, quando o bloco se desloca , uma força de reação age no bloco e o resultado é uma deformação na mola que pode ser obtida através do teorema de Pitágoras:
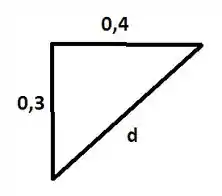
m
Passo 2
Por definição, sabemos que a força devido a deformação de uma mola é calculada por:
Sendo a rigidez da mola e sua deformação.
Podemos verificar que a deformação que a mola sofreu durante o deslocamento do bloco é a diferença entre a deformação final e a inicial, ou seja:
Assim, podemos chegar ao valor da força de reação da mola da seguinte forma:
N
Passo 3
O próximo passa é obter a equação do movimento do corpo. Do diagrama de corpo livre, temos:
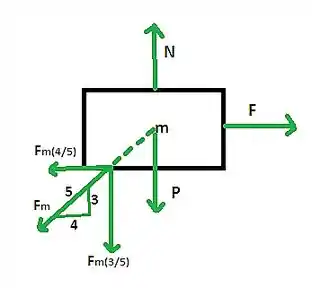
Substituindo o valor da força e da força na equação acima, e isolando a aceleração, temos a seguinte relação:
Resposta
Em , o bloco terá uma aceleração de .