Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 114

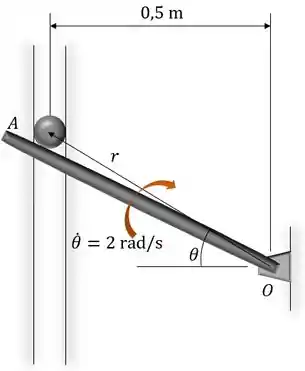
Uma bola de massa de 1 kg e está confinada a se mover ao longo da ranhura vertical lisa devido à rotação do braço liso O A . Determine a força do braço sobre a bola e a força normal da ranhura sobre a bola quando θ = 30 ° . O braço está girando com uma velocidade angular constante de θ ˙ = 3   r a d / s . Suponha que a bola tem contato com apenas um lado da ranhura em qualquer instante.

Passo 1

O enunciado nos dá as seguintes informações:

Massa da bola: m = 1 kg

Velocidade angular constante: θ ˙ = 3 rad/s

A questão pede para determinarmos a força do braço sobre a bola e a força normal da ranhura sobre a bola quando θ = 30 ° .

Desenhamos o seguinte diagrama de corpo livre:

Onde N é a força normal, F O A é a força exercida pela barra e W = m g é a força peso.

Passo 2

Da figura fornecida, vemos que r pode ser relacionada a θ pela equação

cos ⁡ θ = 0,5 r

r = 0,5 cos ⁡ θ

Portanto, as derivadas temporais em r são:

r ˙ = d r d t = 0,5 θ ˙ sen ⁡ θ cos 2 ⁡ θ = 0,5 θ ˙ tan ⁡ θ sec ⁡ θ   m / s

r ¨ = d 2 r d t 2 = 0,5 [ θ ˙ tan ⁡ θ sec ⁡ θ + sec 3 ⁡ θ + tan 2 ⁡ θ sec ⁡ θ θ ˙ 2 ]   m / s 2

Em θ , sabemos que θ ˙ = 3 rad/s é constante, logo

θ ¨ = d θ ˙ d t = 0   r a d / s 2

Para θ = 30 ° :

r = 0,5774   m

r ˙ = 1   m / s

r ¨ = 8,660   m / s 2

Passo 3

Sabemos que as componentes da aceleração nas coordenadas r e θ são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

Logo,

a r = 8,66 - 0,5774 3 2 = 3,464   m / s 2

a θ = 0,5774 0 + 2 1 3 = 6   m / s 2

Passo 4

Aplicaremos as Equações do Movimento.

Analisando no eixo r , temos que

∑ F r = m a r

N cos ⁡ 30 ° - W sen ⁡ 30 ° = m a r

N c o s   30 ° = 1 3,464   + 1 9,81 sen ⁡ 30 °

N = 9,66   N

Analisando no eixo θ , temos que

∑ F θ = m a θ

F O A - N sen ⁡ 30 ° - W cos ⁡ 30 ° = m a θ

F = 1 6 + 9,66 sen ⁡ 30 ° + 1 9,81 cos ⁡ 30 °

F = 19,3   N

Resposta

N = 9,66   N

F = 19,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade angular constante θ ˙ do eixo vertical do brinquedo do parque de diversões se ϕ = 45 ° . Despreze a massa dos cabos e a dimensão dos passageiros.
O pino P de 0,2 kg está restrito a se mover na fenda curva lisa que é definida pela lemniscata r = ( 0,6 cos ⁡ 2 θ ) m. O seu movimento é controlado pela rotação do braço bifurcado O A , o qual tem ve
Uma bola de 0,2 kg é soprada em um tubo circular vertical liso cuja forma é definida por r = ( 0,6 sen ⁡ θ ) m, onde θ é dado em radianos. Se θ = ( π t 2 ) rad, onde t é dado em segundos, determine a
A barra A B de 2 kg desloca-se para cima e para baixo à medida que sua extremidade desliza sobre a superfície lisa do came, onde r = 0,1 m e z = ( 0,02 sen ⁡ θ ) m . Se o came está girando com velocid
Se o coeficiente de atrito estático entre a superfície cônica e o bloco de massa m é μ s = 0,2 , determine a velocidade angular constante mínima θ ˙ de maneira que o bloco não escorregue para baixo.