Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 103

A bola de massa m é submetida a uma velocidade de v A = 5 g r na posição A. Quando ela chega a B , o cabo atinge o pino P, após o que a bola descreve uma trajetória circular menor. Se x = 2 3 r , determine a velocidade da bola e a tração no cabo quando ela está no seu ponto mais alto C.

Passo 1

Primeiramente, deve-se definir a equação da conservação de energia cinética e potencial gravitacional que rege o problema. De forma que :

E A + P A = E C + P C

1 2 m v A 2 + m g h A = 1 2 m v C 2 + m g h B (1)

Passo 2

A velocidade da v C , pode ser obtida ao se desenvolver (1), de modo que :

1 2 m 5 g r 2 + 0 = 1 2 m v C 2 + m g ( 4 3 r )

v C = g r 7 3 (2)

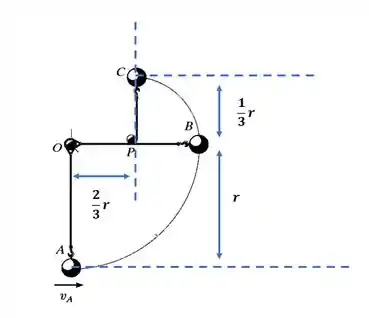
Passo 3

No ponto C, a velocidade escalar da bola pode v C deve ser obtida por meio do somatório das forças que atuam nesse instante, considerando que a corda encontra-se tensionada no fim do movimento. Portanto, têm-se que:

∑ F y = m a y   ∴     F T + F P = m a y

F T + m g = m v C 2 ρ

F T + m g = m g r 7 3 2 r 3

F T = m g r 7 3 r 3 - m g

F T = m 7 g r - m g

F T = 6 m g

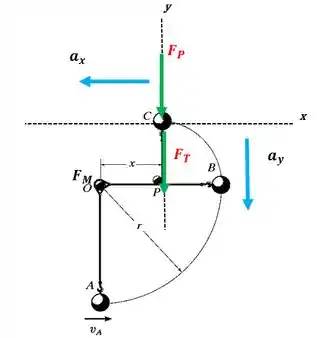
Resposta

De acordo com os passos 1,2, e 3 a velocidade e a força de tração serão respectivamente :

v C = g r 7 3

F T = 6 m g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola tem um comprimento não esticado de 0,4m e uma rigidez de 200N / m . O cursor de 3k g e a mola conectada são liberados a partir do repouso em A e se deslocam no plano vertical. Calcule a velocid
A mola de constante k está sem deformação quando o cursor de massa m passa a posição B . Se o cursor é liberado a partir do repouso na posição A , determine sua velocidade quando este passa pelos pont
O cursor de 10k g desliza sobre a haste vertical lisa e tem uma velocidade v 1 = 2m / s na posição A onde cada mola está esticada de 0,1m . Calcule a velocidade v 2 do cursor quando este passa o ponto
Os pequenos corpos A e B , cada um com massa m , estão ligados e suportados pelas conexões articuladas de massa desprezível. Se A é liberado a partir do repouso na posição mostrada, calcule sua veloci
O êmbolo de 2k g é liberado a partir do repouso na posição mostrada onde a mola de rigidez k = 500N / m foi comprimida para a metade do seu comprimento sem deformação de 200m m . Calcule a altura máxi