Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 156

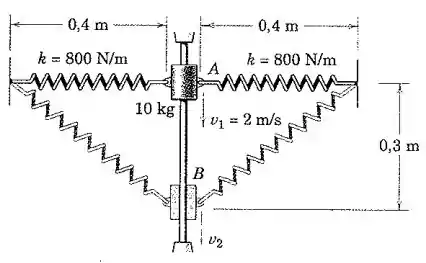
O cursor de 10   k g desliza sobre a haste vertical lisa e tem uma velocidade v 1 = 2   m / s na posição A onde cada mola está esticada de 0,1   m . Calcule a velocidade v 2 do cursor quando este passa o ponto B .

Passo 1

Como em A cada mola está esticada de x 1 = 0,1   m , então o comprimento natural da mola l pode ser obtido assim:

l + x 1 = 0,4

l + 0,1 = 0,4

l = 0,3   m

Então podemos obter a deformação x 2 em B da seguinte forma:

l + x 2 2 = 0,3 2 + 0,4 2

0,3 + x 2 2 = 0,25

x 2 = 0,2   m

Passo 2

Usando a conservação de energia mecânica, obtemos:

Δ T + Δ V g + Δ V e = 0

m 2 v 2 2 - v 1 2 + m g h 2 - h 1 + 2 k 2 x 2 2 - x 1 2 = 0

10 2 v 2 2 - 2 2 + 10 9,81 0 - 0,3 + 2 800 2 0,2 2 - 0,1 2 = 0

5 v 2 2 = 20 + 29,43 - 24

v 2 2 = 5,086

v 2 = 2,26   m / s

Resposta

v 2 = 2,26   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 14.8 utilizando a equação de conservação de energia.
Um recipiente de massa desprezível está ligado a duas molas idênticas de rigidez k= 250 N/m. Se uma caixa de 10 kg é solta de uma altura de 0,5 m acima do recipiente, determine o deslocamento vertical
O homem na bicicleta tenta dar a volta no loop elipsoidal sem sair da pista. Determine a velocidade que ele tem de manter em A imediatamente antes de entrar no loop a fim de realizar a proeza. A bicic
O esquiador de 65 kg parte do repouso em A. Determine sua velocidade em B e a distância s onde ele pousa em C. Despreze o atrito.
O bloco A de 10 kg é solto do repouso e desliza para baixo pelo plano liso. Determine a compressão x da mola quando o bloco para instantaneamente.