Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 151
O êmbolo de é liberado a partir do repouso na posição mostrada onde a mola de rigidez foi comprimida para a metade do seu comprimento sem deformação de . Calcule a altura máxima acima da posição inicial alcançada pelo êmbolo.
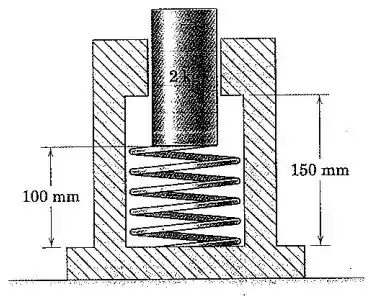
Passo 1
Galera, como a energia mecânica do sistema se conserva, teremos:
Como o êmbolo é liberado a partir do repouso e tem velocidade nula na altura máxima,
A variação de energia potencial elástica será:
Já a variação de energia potencial gravitacional é calculada assim:
Passo 2
Então, teremos o seguinte:
Resposta
Exercícios de Livros Relacionados
49. A porta da garamgem CD tem massa de 50 kg e pode ser tratada como uma placa fina. Determine o comprimento não deformado requereido de cada uma das duas molas laterais quando a porta estiver na pos
52. A placa quadrada de 25kg está presa por um pino no canto A e fixada a uma mola tendo rigidez k = 300 N/m. Se a placa é liberada do repouso quando θ = 0 ° , determine sua velocidade angular quando
55. O painel de porta retangular de 50 kg é mantido na posição vertical pela barra BC. Quando a barra é removida, o painel se fecha devido ao próprio peso. O movimento do painel é controlado por uma m
53. Uma mola com rigidez k = 300 N/m está fixada à extremidade de uma barra de 15 kg, e não está deformada quando θ = 0 ° . Se a barra é liberada do repouso quando θ = 0 ° , determine sua velocidade a
58. A mola torcional em A tem rigidez k = 900 N m/ rad e está deformada quando θ = 0 ° . Determine a velocidade angular das barras, AB e BC, quando θ = 0 ° , se elas são soltas do repouso na posição f