Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 61
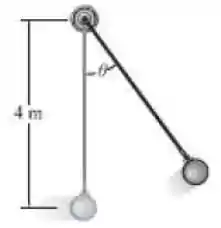
Se a bola tem massa de e uma velocidade de no instante em que ela está no ponto mais baixo, , determine a tração da corda neste instante. Além disso, determine o ângulo até o qual a bola oscila e momentaneamente para. Despreze a dimensão da bola.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Temos dois problemas nesta questão. Precisamos determinar a tração no momento em que . Depois, precisamos determinar o ângulo máximo que ele atinge (logo, a velocidade é nula neste momento!).
Passo 2
Vamos trabalhar inicialmente a primeira parte da questão. Portanto, vamos esboçar o diagrama de corpo livre quando a bola está no seu ponto mais baixo. Logo, temos:
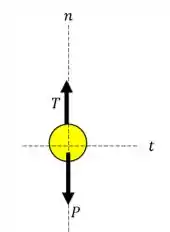
Portanto, a bola está sujeita apenas a uma força de tração e a força peso na direção normal.
Passo 3
Como a bola possui uma componente normal da aceleração na direção normal, temos o seguinte somatório de forças:
Passo 4
Agora vamos fazer o diagrama de corpo livre para a segunda parte da questão. Temos então:
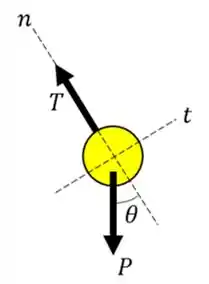
A única mudança é uma mudança na direção do eixo normal. Como a força peso é sempre para baixo e a tração da corda é na direção normal, temos uma mudança no somatório das forças.
Passo 5
Vamos fazer um somatório de forças na direção tangencial. Desta forma, temos:
Para descobrirmos o valor de , vamos ter de voltar as equações da cinemática. O ângulo máximo será atingido no momento em que a velocidade da bola for nula. Lembrando a equação que relaciona aceleração e velocidade através da posição da partícula, temos:
Como , podemos mudar a variável da integral. Para isto, basta fazermos e mudarmos os limites de integração. Obtemos então: