Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 3

O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o raio de giração k x . A densidade do material é ρ = 5 Mg/m3.

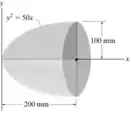
Passo 1

Iremos considerar um d x bem pequeno no eixo x . Sabemos que sabemos que d m = ρ . d V , então, para a figura dada, podemos considerar d m = ρ π   y 2   d x = ρ π 50 x d x .

Passo 2

Vamos encontrar o momento de inércia para o eixo x . Então,

I x = ∫ 1 2 y 2 d m = 1 2 ∫ 0 200 50 x π ρ 50 x d x =

= ρ π 50 2 6 200 3

Passo 3

Iremos calcular a massa, ou seja, m = ∫ d m = ∫ 0 200 π ρ 50 x d x = ρ π 50 2 200 2

Passo 4

Pela teoria, sabemos que k x = I x m . Então,

k x = ρ π 50 2 6 200 3 ρ π 50 2 200 2 = 50 3 200 = 57,7 mm

Resposta

k x = 57,7 mm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As rodas A e B têm uma massa de 75 kg e 50 kg, respectivamente. Inicialmentem a roda A gira no sentido horário com uma velocidade angular constante de ω = 100 rad/s e a roda B está em repouso. Se A é
A roda de 100 kg tem um raio de giração em relação a seu centro O k O = 500m m . Se a roda parte do repouso, determine sua velocidade angular em t = 3 s.
No instante mostrado, o disco de 30 kg tem uma velocidade angular no sentido anti-horário de ω = 10r a d / s . Determine as componentes normais e tangenciais da reação do pino O sobre o disco e a acel
A barra fina uniforme de 30 kg está sendo puxada pela corda que passa sobre o pino liso pequeno em A. Se a barra tem uma velocidade angular de ω = 6r a d / s no instante mostrado, determine as compone
O disco de 50 kg está submetido ao momento de binário M = (9t) N.m, onde t é dado em segundos. Determine a velocidade angular do disco quando t = 4 s partindo do repouso.