Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.1 - Ex. 3

Para os vetores   V → 1 e    V → 2 dados, determine V 1 + V 2 , V → 1 + V → 2 , V 1 → - V → 2 , V 1 → × V 2 → , V 2 → × V 1 → e V 1 → ∙ V 2 → . Considere que os vetores sejam adimensionais.

Passo 1

Vamos por partes. O primeiro objetivo é calcular a soma dos módulos dos vetores. Sem problemas, esses valores já foram dados:

V 1 + V 2 = 15 + 12 = 27

Como disse o enunciado, os vetores são adimensionais, então não temos unidades de medida.

Passo 2

Para as próximas perguntas, precisamos achar as componentes x e y dos vetores.

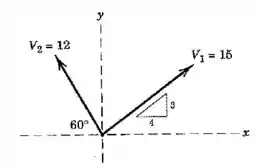
Para o V 1 → a imagem já dá a dica, pois sugere que a gente utilize a proporção 3 ,   4 e 5 do triângulo retângulo. Você deve lembrar pelo menos das duas mais comuns:

3 2 + 4 2 = 5 2

9 2 + 12 2 = 15 2

Então as duas coordenadas do vetor V 1 → são 9 e 12 , mas qual delas é x e qual é y ? O enunciado também já deu essa dica, pois a imagem mostra que a coordenada y do vetor é a menor, então:

V 1 = ( 12,9 )

E para achar as coordenadas de V 2 → , é só tirar proveito daquele ângulo de 60 ° e acertar os sinais!

V 2 → = - 12 cos ⁡ 60 ° , 12 sen ⁡ 60 ° = - 12   . 1 2   ,   12   . 3 2 = ( - 6,6 3 )  

Ok, agora podemos fazer as contas.

Passo 3

Então a soma dos vetores vai ficar assim:

V 1 → + V 2 → = 12,9 + - 6,6 3 = ( 6   ,   9 + 6 3 )

Isso porque, para somar vetores, nós temos que somar cada uma das componentes. Agora tomando os valores numéricos:

V 1 → + V 2 → = ( 6   ,   19,39 )

V 1 → + V 2 → ≅ 6   i ^ + 19,39 j ^

E para a diferença de vetores o cálculo é muito parecido:

V 1 → - V 2 → = 12,9 - ( - 6   ,   6 3 )

V 1 → - V 2 → = 18 i ^ - 1,39 j ^

Passo 4

Para o produto vetorial a coisa fica um pouco mais complicada. A forma mais fácil de calcular é usar essa definição aqui:

V 1 → × V 2 → = i ^ j ^ k ^ V 1 x V 1 y V 1 z V 2 x V 2 y V 2 z = i ^ j ^ k ^ 12 9 0 - 6 6 3 0

Ou seja, calcular o produto vetorial como se fosse o determinante de uma matriz. Se você não lembra como se calcula o determinante de uma matriz 3 × 3 , é uma boa ideia relembrar.

Fazendo os cálculos, vamos chegar na seguinte resposta:

V 1 → × V 2 → = k ^ 72 3 + 54 ≅ 178,7   k ^

Ok, isso é V 1 → × V 2 → , mas e V 2 → × V 1 → ? É só lembrar que o produto vetorial é anticomutativo! Isso quer dizer o seguinte:

( A → × B → ) = - ( B → × A → )

Ou seja:

V 2 → × V 1 → = - 178,7   k ^

Passo 5

Agora falta calcular o produto interno. A fórmula é essa aqui:

x 1 , y 1 ∙ x 2 , y 2 = x 1 x 2 + y 1 y 2

Ou seja:

V 1 → ∙ V 2 → = 12   ,   9 ∙ - 6   ,   6 3 = 12 - 6 + 9 6 3 = - 72 + 54 3

V 1 → ∙ V 2 → ≅ 21,5

Resolvido!

Resposta

V 1 + V 2 = 27

V → 1 + V → 2 = 6   i ^ + 19,39 j ^

V 1 → - V → 2 = 18 i ^ - 1,39 j ^

V 1 → × V 2 → = 178,7   k ^

V 2 → × V 1 → = - 178,7   k ^

V 1 → ∙ V 2 → = 21,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um vagão ferroviário de carvão possui uma massa de 25t vazio transporta uma carga total de 90t de carvão. Os compartimentos são equipados com portas no fundo que permitem o descarregamento do carvão a
A extremidade superior da corrente de elos de comrpimento L e massa ρ por unidade de comprimento é abaixada a uma velocidade constante v pela força P . Determine a leitura R da balança de plataforma e
Em uma estação de carregamento a granel, o cascalho sai do funil alimentador na taxa de 100k g / s com uma velocidade de 3m / s na direção mostrada e é depositado sobre o caminhão plataforma em movime
A figura representa uma estrutura unidimensional idealizada de massa uniforme ρ por unidade de comprimento de deslocando horizontalmente com uma velocidade v 0 quando sua extremidade dianteira colide
4/110) A bomba centrífuga processa 20m 3 de água doce por minuto com velocidades de entrada e de saída de 18 m / s . O impelidor gira no sentido horário através do eixo em O acionado por ummotor que f