Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 107

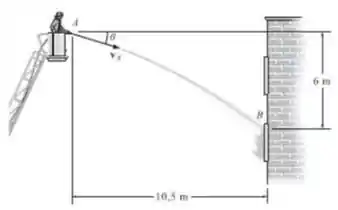
Um bombeiro quer direcionar o fluxo de água da sua mangueira para o fogo em B. Determine dois ângulos possíveis θ 1 e θ 2 nos quais isso pode ser feito. A água sai da mangueira a v A = 24   m / s .

Passo 1

Este é um problema bem interessante. Ele já nos deixa claro que temos dois possíveis ângulos que resolve o nosso problema. O primeiro deles é bastante sugestivo, pois basta observar a imagem da nossa questão. Já o segundo, pode nos causar dúvida. Mas na verdade ele é bem simples também! Basta inclinar nossa mangueira para cima. A água irá subir e posteriormente cair, atingindo o ponto B.

Para resolvermos esta questão, vamos considerar o ângulo θ medido no sentido horário a partir do eixo x , conforme mostrado na figura da questão. Para descobrirmos os valores dos ângulos θ que satisfazem o nosso problema, precisamos resolver as equações da cinemática na direção do eixo x e na direção do eixo y . Isto é, vamos dividir para conquistar!

Passo 2

Vamos começar por trabalhar com a direção do eixo x . Nesta direção, o jato de água não está sujeito a nenhuma aceleração. Portanto, ao trabalharmos com as equações de posição, teremos:

s = s 0 + v x t

10,5 = 0 + v A ⋅ cos ⁡ θ t

10,5 = 0 + 24 ⋅ cos ⁡ θ t

t = 10,5 24 ⋅ cos ⁡ θ

Portanto, conseguimos determinar uma relação entre o tempo e o ângulo θ . Precisamos de uma outra equação que relacione estes dois parâmetros para que possamos resolver a questão. Para consegui-la, precisaremos trabalhar com as equações da cinemática na direção do eixo y .

Passo 3

Na direção do eixo y , temos a ação da gravidade para baixo. Portanto, a equação da posição do jato será dada por:

s = s 0 + v y t + a t 2 2

- 6 = 0 - v A ⋅ sen ⁡ θ ⋅ t - g t 2 2

- 6 = - 24 ⋅ sen ⁡ θ ⋅ 10,5 24 ⋅ cos ⁡ θ - 4,905 10,5 24 ⋅ cos ⁡ θ 2

- 6 cos 2 ⁡ θ = - 10,5 sen ⁡ θ cos ⁡ θ - 0,939

6 cos 2 ⁡ θ = 5,25 sen ⁡ 2 θ + 0,939

Esta é uma equação difícil de resolver analiticamente. Utilizando ferramentas computacionais, determinamos que:

θ 1 = 24,8 °

θ 2 = - 85,1 °

O sinal positive do ângulo θ 1 indica que ele está na direção que começamos a medir o ângulo θ . Isto é, ele é voltado para baixo. Já o ângulo θ 2 é voltado para cima

Resposta

Voltado para baixo temos o ângulo θ 1 = 24,8 ° . Já voltado para cima temos o ângulo θ 2 = - 85,1 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a posição de uma partícula é definida por s = 2 sen ⁡ π 5 t + 4 m , onde t é dado em segundos, construa os gráficos s - t , v - t e a - t para 0 ≤ t ≤ 10 s.
Um míssil de dois estágios é lançado verticalmente a partir do repouso com a aceleração mostrada. Em 15 s, o primeiro estágio A esgota-se e o segundo estágio B dá partida. Elabore os gráficos v - t e
As cavilhas A e B estão restritas a moverem-se nas fendas elípticas devido ao movimento da fenda da barra. Se a fenda da barra se desloca com uma velocidade escalar constante de 10 m/s, determine a in
A cavilha P é inpulsionada pelo anel do garfo O A ao longo da trajetória curva descrita por r = ( 2 θ ) m. No instante θ = π / 4 rad, a velocidade angular e a aceleração angular do anel garfo são θ ˙
O carro tem uma velocidade escalar de 16.5 m/s. Determine a velocidade angular θ ˙ da linha radial O A nesse instante.