Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 64

Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considerado como um ponto de massa concentrada. Determine as componentes verticais e horizontais da reação no pino B se a gôndola balança livremente a ω = 1 rad/s quando ela alcança seu ponto mais baixo, como mostrado. Além disso, qual é a aceleração angular da gôndola nesse instante?

Passo 1

Vamos considerar a aceleração da gravidade como g = 9,81   m / s 2 .

Começaremos analisando o momento de inércia da gondola e do contra peso com relação ao ponto B:

I B = m B k B 2 + m a ç o r a ç o 2

I B = 50 10 3 3,5 2 + 3 10 3 3 2

I B = 639,5 10 3 k g . m 2

Passo 2

Agora, iremos decompor a aceleração em suas componentes normais e tangenciais com o auxílio da figura a seguir.

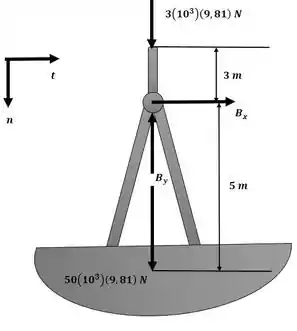
O componente normal da gôndola é dado por:

a G n g = ω 2 r g = 1 2 5 → a G n g = 5   m / s 2

O componente normal do contra peso é dado por:

a G n C = ω 2 r C = 1 2 3 → a G n C = 3   m / s 2

A componente tangencial da aceleração da gôndola é dada por:

a G t g = α r g = 5 α

A componente tangencial da aceleração do contra peso é dada por:

a G t C = α r C = 3 α

Passo 3

Agora, iremos aplicar o somatório de momentos em torno do ponto B:

↺ + ∑ M B = I B α

0 = 639,5 10 3 α → α = 0

Aplicando o somatório de forças na direção tangencial:

+ → ∑ F t = m a G t

B x = 0

+ ↓ ∑ F n = m a G n

3 10 3 9,81 + 50 10 3 9,81 - B y = 3 10 3 3 - 50 ( 10 3 ) ( 5 )

B y = 761   k N

Resposta

α = 0

B x = 0

B y = 761   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cone circular reto de altura h e raio da base r gira em torno de seu eixo de simetria com uma velocidade angular p . Simultaneamente, o cone inteiro gira em torno do eixo x com velocidade angular Ω
A bobina A gira em torno de seu eixo com uma velocidade angular de 20rad/s, inicialmente no sentido de w0 e em seguida no sentido de ws. Simultaneamente, o conjunto gira em torno do eixo vertical com
Um disco circular gira em torno de um eixo fixo com uma velocidade angular constante ω =10 i + 2 j + 2 k r a d / s . Em um determinado instante, um ponto P sobre sua borda possui uma velocidade cujas
O conjunto de painéis e os eixos vinculados x-y-z giram com uma velocidade angular constante Ω = 0,6r a d / s em torno do eixo vertical z. Simultaneamente, os painéis giram em torno do eixo y como mos
Se o motor gira em torno do eixo x na taxa constante γ ˙ = 3 π r a d / s , sem rotação em torno do eixo Z, determine a aceleração angular do rotor e do disco no instante em que a posição γ = 30 ° é cr