Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 43
Um míssil de dois estágios é lançado verticalmente a partir do repouso com a aceleração mostrada. Em 15 s, o primeiro estágio esgota-se e o segundo estágio dá partida. Elabore os gráficos e que descrevem, o movimento dos dois estágios do míssil para s.
Passo 1
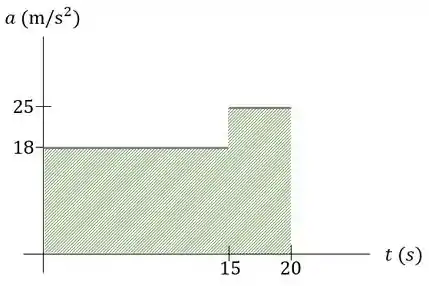
O gráfico dado pelo enunciado é o gráfico aceleração-tempo .
A partir desse gráfico, atráves da relação
onde a variação da velocidade é igual a área sob o gráfico , podemos construir o gráfico
A partir do gráfico , através da relação
Onde a variação do deslocamento é igual a área sob o gráfico , podemos construir o gráfico
Passo 2
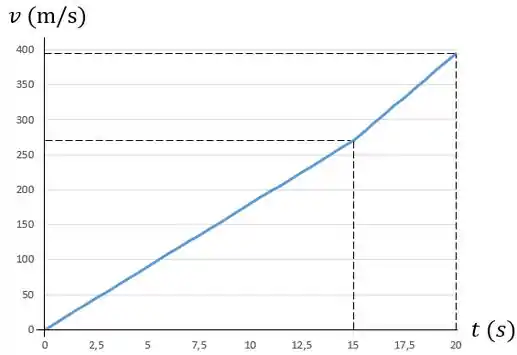
Primeiramente, vamos desenhar o gráfico .
Temos que,
Em s, m/s.
No intervalo :
No instante s:
No intervalo :
No instante s:
Plotanto esses pontos no gráfico, obteremos
Passo 3
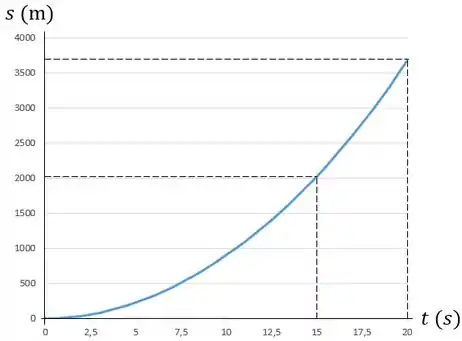
Em seguida, vamos desenhar o gráfico .
Temos que,
Em s, m/s.
No intervalo :
No instante s:
No intervalo :
No instante s:
Plotanto esses pontos no gráfico, obteremos
Resposta
Ei, a resposta está no passo a passo :)