Se a posição de uma partícula é definida por s = 2 sen ⁡ π 5 t + 4 m , onde t é dado em segundos, construa os gráficos s - t , v - t e a - t para 0 ≤ t ≤ 10 s.

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 45

Se a posição de uma partícula é definida por , onde é dado em segundos, construa os gráficos , e para s.

Passo 1

O enunciado nos fornece a função , logo, para construir o gráfico , basta supor diferente valores para dentro do intervalo fornecido e encontrar os correspondentes valores de .

Gráfico :

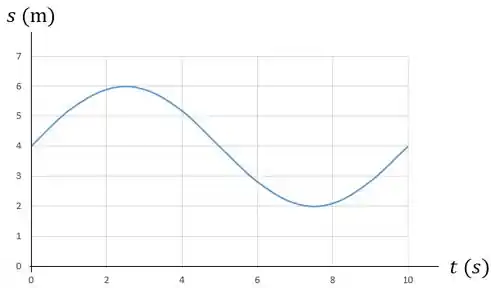
Passo 2

Sabemos que a derivada temporal do espaço é igual a velocidade, ou seja,

Logo,

Para construir o gráfico , basta supor diferente valores para dentro do intervalo fornecido e encontrar os correspondentes valores de .

Gráfico :

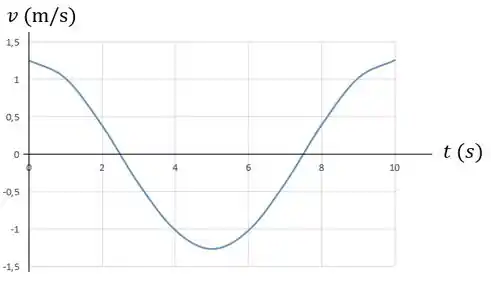
Passo 3

Sabemos que a derivada temporal da velocidade é igual a aceleração, ou seja,

Logo,

Para construir o gráfico , basta supor diferente valores para dentro do intervalo fornecido e encontrar os correspondentes valores de .

Gráfico :

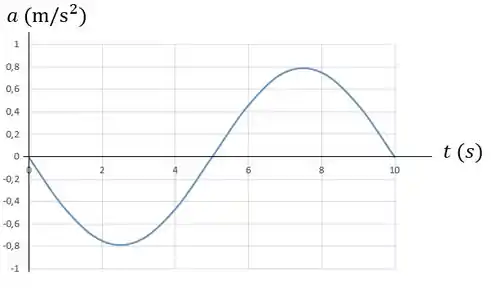
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inclua a resistência do ar para os fardos de feno no problema anterior. Um fardo de feno tem massa aproximada de 30k g e área de cerca de 0,2m 2 . Considere a resistência do ar proporcional ao quadrad

Inclua a resistência do ar proporcional ao quadrado da velocidade da bola no problema anterior. Considere o coeficiente de arrasto como sendo c w = 0,5 , o raio da bola igual a 5c m e sua massa 200g .

Um cubo sólido de densidade uniforme e lados com dimensão b se encontra em equilíbrio na parte superior de um cilindro de raio R (Figura 2.C). Os planos dos quatro lados do cubo são paralelos ao eixo

Uma partícula se move em órbita bidimensional definida por: x t = A 2 α t - s e nα t y t = A ( 1 - cos ⁡ α t ) Determine a aceleração tangencial at, e a aceleração normal an, como uma função do tempo,

Um canhão se localiza sobre uma elevação de altura h sobre o vale de um rio. Se a velocidade de disparo na boca do canhão é v0, determine a expressão para o alcance em função do ângulo de elevação da