Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 35
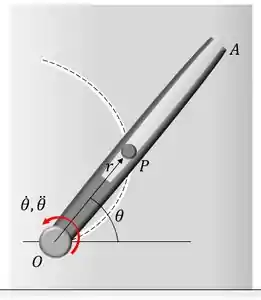
A cavilha é inpulsionada pelo anel do garfo ao longo da trajetória curva descrita por m. No instante rad, a velocidade angular e a aceleração angular do anel garfo são rad/s e rad/s2. Determine a intensidade da aceleração da cavilha nesse instante.
Passo 1
O enunciado nos dá as seguintes informações:
Trajetória curva: m;
Velocidade angular do anel do garfo: rad/s;
Aceleração angular do anel do garfo: rad/s2.
Devemos determinar a intensidade da aceleração da cavilha no instante rad.
A velocidade angular e a aceleração angular da cavilha são iguais as do anel do garfo, pois ambas se movem juntas.
Passo 2
Vamos encontrar a intensidade da aceleração da cavilha.
Sabemos que, por definição, a aceleração em coordenadas polares é composta por uma componente radial e uma componente transversal, conforme exibido abaixo:
Onde
Logo, para encontrar o valor de , precisamos definir quem são e Os valores de e já são dados pela questão.
Sabendo que , suas derivadas temporais são
Logo, em , obtemos
As componentes radial e transversal da aceleração em são:
A intensidade de é dada por