Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 62
O borrifador é projetado para girar à velocidade angular constante e espalhar água na taxa volumétrica . Cada um dos quatro bocais tem uma área de saída . Escreva uma expressão para o torque sobre o eixo do borrifador necessário para manter o movimento requerido. Para uma determinada pressão e, consequentemente, uma taxa de fluxo , a que velocidade irá operar o borrifador sem nenhum torque aplicado? Seja a massa específica da água.
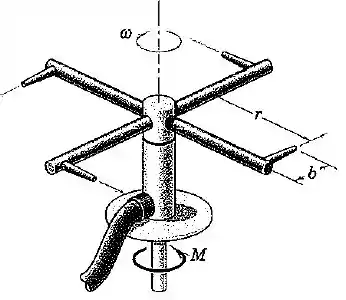
Passo 1
Vamos calcular o momento em relação ao eixo do borrifador. A fórmula que precisamos usar é a seguinte:
Como a água entra no sismte através do próprio eixo, a velocidade de entrada está na própria direção do nosso ponto de referência, então :
Se a taxa volumétrica é , podemos calcular a taxa de escoamento de massa através da massa específica :
Então nossa fórmula fica:
Passo 2
Se a água deixa o cano de área a uma taxa volumétrica , isso significa que a velocidade de saída da água em cada cano é:
Essa é a velocidade da água em relação ao cano. Mas como o cano em si também está girando, precisamos descontar a velocidade que a água adiqure ao participar desse movimento.
Substituindo isso na nossa equação para o momento resultante, vamos ficar com a seguinte expressão:
E então:
Passo 3
E para encontrar a velocidade angular no caso em que nenhum momento é aplicado podemos aproveitar a expressão que acabamos de escrever:
Estamos interessados no caso :
Isolando :
Resposta
O torque necessário é , e na sua ausência a velocidade angular do movimento seria .