Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 41

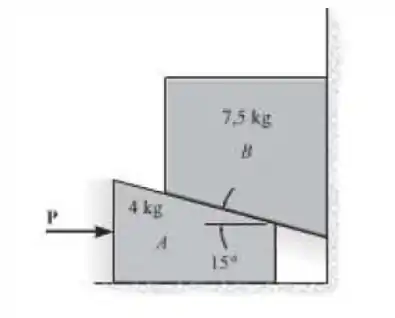
Se uma força horizontal de P = 50   N é aplicada ao bloco A determine a aceleração do bloco B. Despreze o atrito. Dica: mostre que a B = a A tg ⁡ 15 °

Passo 1

Vamos seguir a dica do nosso problema. Já temos uma equação que relaciona a aceleração dos dois blocos. Caso queira provar que é verdade, basta fechar um triângulo retângulo no qual os catetos são os comprimentos s B e s A , relativos ao deslocamento de cada um dos blocos.

Para resolvermos a nossa questão, precisaremos esboçar o diagrama de corpo livre de ambos os blocos. A partir da nossa análise da cinética, e também do uso da dica da questão, conseguiremos determinar a aceleração do bloco B.

Passo 2

Vamos começar fazendo uma análise do bloco A. Seu diagrama de corpo livre é:

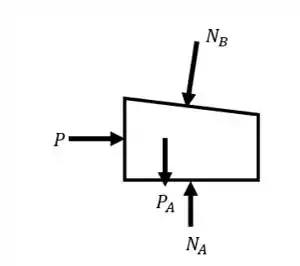
Fazendo o somatório das forças no eixo x , teremos:

→ ∑ F x = m ⋅ a x

P - N B sen ⁡ 15 = m a A

50 - N B sen ⁡ 15 = 4 a A

N B = 50 - 4 a A sen ⁡ 15

Passo 3

Já para o bloco B, teremos:

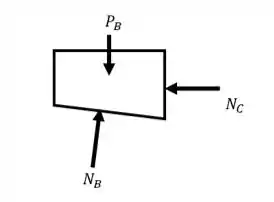
Fazendo o somatório das forças no eixo y , teremos:

↑ ∑ F y = m ⋅ a y

N B cos ⁡ 15 - P B = 7,5 a B

N B cos ⁡ 15 - 7,5 ⋅ 9,81 = a B

a B = N B cos ⁡ 15 7,5 - 9,81

Como sabemos que a B = a A tan ⁡ 15 , temos:

a A = 1 tan ⁡ 15 ⋅ N B cos ⁡ 15 7,5 - 9,81

a A = 1 tan ⁡ 15 ⋅ 50 - 4 a A sen ⁡ 15 ⋅ cos ⁡ 15 7,5 - 9,81

7,5 tan ⁡ 15 sen ⁡ 15 + 4 cos ⁡ 15 a A = 50 ⋅ cos ⁡ 15 - 9,81 ⋅ 7,5 tan ⁡ 15 sen ⁡ 15

a A = 9,852   m / s 2

Logo,

a B = 2,64   m / s 2

Resposta

a B = 2,64   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O coeficiente de arrasto C A de um automóvel é determinado a partir da expressão C A = A 1 2 ρ v 2 S Onde A é a força de arrasto determinada experimentalmente em um túnel de vento, ρ é a massa específ
Para os vetores V → 1 e V → 2 dados, determine V 1 + V 2 , V → 1 + V → 2 , V 1 → - V → 2 , V 1 → × V 2 → , V 2 → × V 1 → e V 1 → ∙ V 2 → . Considere que os vetores sejam adimensionais.
A que altitude h acima do pólo norte o peso de um objeto é reduzido para 10 % do seu valor na superfície terrestre? Assuma a Terra esférica com raio R e expresse h em termos de R .
Determine a razão R A da força exercida pelo Sol sobre a Lua por aquela exercida pela Terra sobre a Lua para a posição A da Lua. Repita para Lua na posição B .
As três esferas com 100m m de diâmetro constrúidas com diferentes metais estão localizadas nos vértices de um triângulo equilátero no espaço profundo. Determine a resultante R das forças gravitacionai