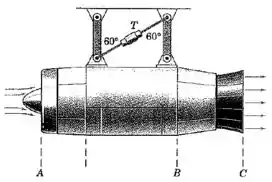
No teste estático do conjunto de um motor a jato e um bocal de exaustão, o ar é sugado para o motor na taxa de e o combustível é quimado na taxa de . A área de escoamento, a pressão estática, e a velocidade axial de escoamento para as três seções indicadas são as seguintes:

Determine a tração no membro na diagonal do suporte do banco do ensaio e calcule a força exercida sobre o flange do bocal em pelos parafusos e pela vedação para sustentar o bocal no alojamento do motor.

Na direção horizontal nós temos três forças contribuindo para o escoamento do fluido: as pressões estáticas nas duas aberturas, e a tração (que mantém a estrutura do motor intacta diante da força que o escoamento faz contra as paredes).

Mas não esqueça de projetar tudo na direção horizontal! Então ficamos com o seguinte:

E o sinal negativo aparece antes dos termos que são contrários ao escoamento do líquido. Agora vamos substituir os valores:

Agora podemos voltar à nossa equação incial para encontrar :

E agora precisamos encontrar a força exercida sobre o flange (que é uma espécie de contector) do bocal .

Basicamente o que vamos fazer aqui é repetir os cálculos que acabamos de fazer, mas olhando apenas para o trecho de saída entre os bocais e .

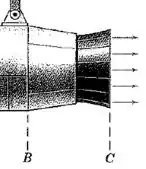
Seguindo a mesma lógica de antes:

Vamos começar escrevendo o termo da esquerda:

E o termo da direita é:

Podemos olhar os dados na tabela e substituir na equação:

Pronto!