Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 16
Se o boxeador bate no saco de pancada de 75 kg com um impulso I = 20 N.s, determine a velocidade angular do saco imediatamente após ele ser atingido. Determine também a localização d do ponto B, em torno do qual o saco parece girar. Trate o saco como um cilindro uniforme.
Passo 1
Para resolver esse exercício, iremos considerar a aceleração da gravidade .
Devemos começar o exercício calculando o momento de inércia do saco, que será utilizado no princípio do impulso e momento, sendo assim:
Passo 2
Aplicando o princípio do impulso e momento linear na direção x com o auxílio da imagem a seguir, conseguimos determinar a velocidade final do centro de massa do saco, sendo assim:
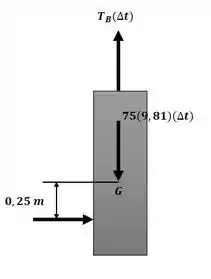
Agora, aplicando o mesmo princípio para o movimento angular, podemos encontrar a velocidade angular do saco um instante após o soco:
Passo 3
Agora, sabendo que a velocidade linear do centro de massa se relaciona com a angular da seguinte forma:
Podemos susbtituir os valores já encontrados para determinar a altura d conforme ilustrado no esquema a seguir:
