Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 37
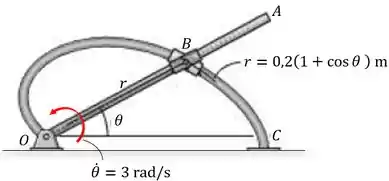
Os anéis estão conectados por um pino em e estão livres para se mover ao longo da barra e da guia curvilínea , tendo o formato de uma cardinoide, m. Em , a velocidade angular de é rad/s. Determine as intensidades da velocidade dos anéis nesse ponto.
Passo 1
O enunciado nos dá as seguintes informações:
Trajetória : ;
Trajetória : m;
Devemos determinar as intensidades da velocidade dos anéis quando .
Neste ponto, a velocidade angular é rad/s.
Considerando que oa anéis estão conectados e sempre andarão juntos, a velocidade será a mesma para ambos. Além disso, ambos farão a mesma trajetória . Como nós a conhecemos, resolveremos a questão a partir dela.
Passo 2
Vamos lá encontrar a intensidade da velocidade !
Sabemos que, por definição, a velocidade em coordenadas polares é composta por uma componente radial e uma componente transversal, conforme exibido abaixo:
Onde
Logo, para encontrar o valor de , precisamos definir quem são e . O valor da velocidade angular já é dado pela questão, logo precisamos apenas encontrar o valor de
Sabendo que , sua derivada temporal será
Logo, as componentes radial e transversal da velocidade são:
Em , temos
A intensidade de é dada por