Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 121
A velocidade inicial do bloco na posição A é 9 m/s. Sabendo que o coeficiente de atrito cinético entre o bloco e o plano é , determine o tempo que o bloco leva para atingir B com velocidade zero se (a) , (b) .
Passo 1
Primeiro, vamos resolver a letra a. Para isso, sempre se faz necessário o uso do diagrama de corpo livre para a visualização das forças atuantes sobre os corpos. Para um plano sem inclinação (), temos a seguinte configuração de forças:
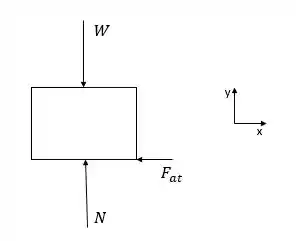
Para calcular o tempo que o bloco se desloca do ponto A para o ponto B, usaremos o princípio do impulso e da quantidade de movimento, dado por:
Onde . Para este problema, .
Passo 2
Agora, vamos calcular . Como N = W, e nesse caso deve-se considerar a direção de aplicação da força seja igual à direção do movimento, o impulso é dado por:
Substituindo na equação descrita no passo 1 para a quantidade de movimento linear, temos que o tempo do deslocamento entre A e B será:
Passo 3
Para a letra b, o diagrama de corpo livre para é representado por:
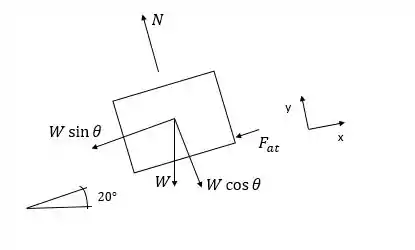
Assim, pelo princípio do impulso e da quantidade de movimento angular, temos que, para as componentes em x:
Resposta
- t = 3,06 s
- t = 1,47 s