Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 136
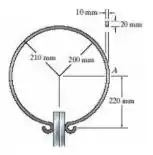
A braçadeira circular de mola produz uma força de compressão de 3 N sobre as chapas. Determine a tensão de flexão máxima produzida na mola A. A mola tem seção transversal retangular, como mostra a figura.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questãozinha nos mostra essa argolinha e nos pede para calcular o valor da tensão máxima, que pode ser tanto de tração quanto de compressão, mas vamos calcular as duas para descobrir. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!
Passo 2
Nosso primeiro passo será calcular a área e o r’.
A = 20 x 10 = 200 mm²
r’ = 200 + 5 = 205 mm
Feito isso, precisamos determinar a localização do centroide, que é medida em ação ao centro de curvatura, seguido pelo cálculo do eixo neutro. Como nossa estrutura pode ser dividida em vários pedacinhos com partes compostas, podemos integrar tudo.
mm
R = = mm
Passo 3
Pronto, nossos pontos mais difíceis da questão já foram resolvidos. Só falta calcularmos o nosso momento e as tensões em cada extremidade do corte.
∑ M = 0 ∴ M – 3 x 0,22 = 0 ∴ M = 0,66 N.m
σa = = 2,01 MPa
σb = = - 1,95 MPa
Resposta
σa = 2,01 MPa – tração