Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 67

Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante vertical V aplicada em O.

Passo 1

Galerinha, o enunciado pede que a gente determine a localização do centro de cisalhamento O. Vamos começar calculando a relação área, diâmetro inércia como o quadro abaixo :D

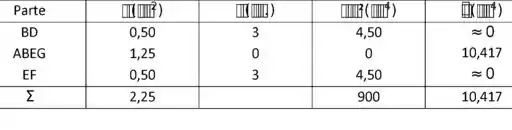
A inércia geral do sistema temos:

I =   Σ A d 2 + Σ I   _ =   19,417   i n 4

Passo 2

Agora gurizada vamos para a letra A , considerando a seção BD, vem comigo :D. Considere o esboço abaixo :D

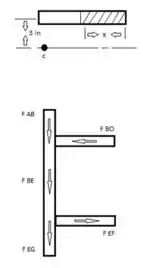
(a) Parte BD:

Q x = 3 t x

q x = V Q x I = V I ( 3 t x )

F = 3 V t I ∫ 0 4 x d x = 3 V t I 8 = 24 V t I

Seu momento sobre H:

( M B D ) H = 3 F B D = 72 V t I

Passo 3

Parte EF: Pelo mesmo método,

F E F = 24 V t I                                             ( M E F ) H = 72 V t I  

Momentos de F A B ,   F B E , e   F E G   sobre H são zero.

V e = Σ M H = 72 V t I + 72 V t I = 144 V t I

e = 144 V t I =   ( 144 ) ( 0,125 ) 19,417

e = 0,927   i n .

Passo 4

Agora vem comigo para resolvermos a letra B :D

(b) Em A, D, F, e G,

Q=0                                             τ A = τ D = τ F = τ G = 0

Logo acima de B:

Q 1 = Q A B = 2 t 4 = 8 t

τ 1 = V Q 1 I t = 2,75 8 t 19,417 t     = 1,133   k s i  

Logo a direita de B:

Q 2 = Q B D = 3 t 4 = 12 t

τ 2 = V Q 2 I t = 2,75 12 t 19,417 t = 1,700   k s i

Passo 5

Não desistam de mim falta pouco

Logo abaixo de B:

Q 3 = Q 1 + Q 2 = 20 t

τ 3 = V Q 3 I t = 2,75 20 t 19,417 t = 2,83   k s i

Em H (eixo neutro),

Q H = Q 3 + Q B H = 20 t + t 3 1,5 = 24,5 t

τ H = V Q H I t = 2,75 24,5 t 19,417 t = 3,47   k s i

Por simetria,

τ 4 = τ 3 = 2,83   k s i

τ 5 = τ 2 = 1,700 ksi

τ 6 = τ 1 = 1,133   k s i

Resposta

τ 4 = τ 3 = 2,83   k s i

τ 5 = τ 2 = 1,700 ksi

τ 6 = τ 1 = 1,133   k s i

:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.
Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.
A viga em balanço AB, consistindo na metade de um tubo de paredes finas com raio médio de 31,8mm e espessura de parede de 9,53mm, está submetida a uma força vertical de 2224 kN. Sabendo que a linha de
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante