Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 89
Três pranchas são pregadas juntas de modo a formar a viga mostrada, a qual está submetida a uma força cortante vertical. Sabendo que o espaçamento entre os pregos é e a força cortante admissível em cada prego é de ,determine a força cortante admissível quando .
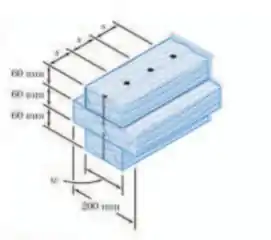
Passo 1
E ai galerinha tudo belezinha? O enunciado pede que a gente determine a força cortante admissível quando ., para isso primeiramente vamos desenhar um diagrama de corpo livre :D.
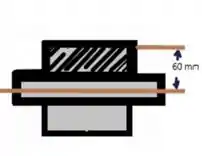
Passo 2
Agora devemos calcular a inércia do elemento como um todo a partir da tabela do passo 1
Considerando:
Temos então a força cortante:
Resposta
Exercícios de Livros Relacionados
A viga em balanço mostrada consiste em um Forma Z de 6,4 mm. espessura. Para o carregamento dado, determine a distribuição das tensões de cisalhamento ao longo da linha A’B’ na aba horizontal superior
Determine a localização do centro de cisalhamento O de uma viga de parede fina uniforme espessura tendo a seção transversal mostrada.
Para a viga em balanço e o carregamento do Problema 6,87, determine a distribuição de tensão de cisalhamento ao longo da linha B’D’ na alma vertical do perfil Z.
Determine a localização do centro de cisalhamento O de uma viga de paredes finas de espessuras uniforme com a seção transversal mostrada.
Considere a viga em balanço AB discutida na Seção 6.5 e a parte ACKJ da viga que está localizada à esquerda da seção transversal CC´ e acima do plano horizontal JK, em que K é um ponto a uma distância