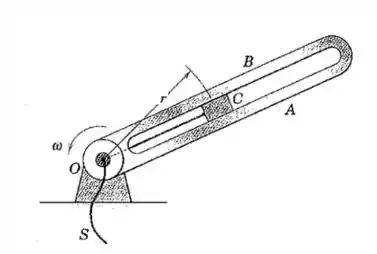
O braço ranhurado gira no plano horizontal em torno do eixo vertical fixo que passa pelo ponto . O cursor de é puxado em direção a na taxa constante de tracionando o cordão . No instante em que , o braço tem uma velocidade angular no sentido anti-horário e que está diminuindo na taxa de . Para esse instante, determine a tração no cordão e o módulo da força exercida sobre o cursor pelas superfícies laterais da ranhura radial lisa. Indique qual lado, ou , da ranhura tem contato com o cursor.

Quando estiver trabalhando com coordenadas polares é uma boa ideia definir as direções tangencial e normal pelo desenho:

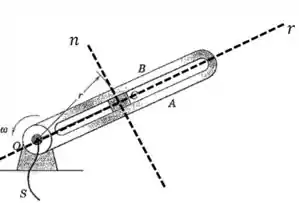
A força de tração está na direção do fio que puxa a massa. E ela é a única força atuando na direção . É importante lembrar que essa imagem é uma visão de cima, portanto a força peso é perpendicular ao plano da página!

E o sinal negativo aparece para respeitar a convenção de que o sentido positivo aponta para longe do centro da trajetória.

E pela fórmula da aceleração radial em coordenadas polares:

E a força normal cumpre um papel bastante parecido: ela é a única força atual na direção !

Nesse caso é a normal “resultante” sobre a massa, já que a princípio as duas paredes do braço poderiam estar exercendo forças de contato em direções opostas uma a outra.

O fato de que é negativo indica que a força normal está apontando no sentido horário, ou seja, ela é a força de contato exercida pela parede !