Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 89
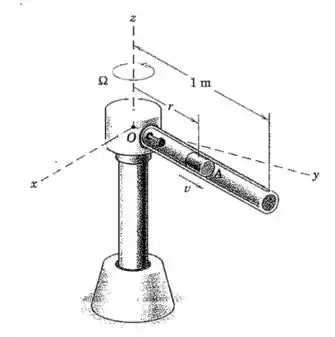
O pequeno cursor de se desloca sem atrito considerável no tubo vazado, que gira em um plano horizontal com uma velocidade constante . O cursor é lançado com uma velocidade inicial em relação ao tubo nas coordenadas inerciais e . Determine o módulo da força horizontal exercida sobre o cursor pelo tubo imediatamente antes de o cursor sair do tubo.
Passo 1
Como não existe força de atrito entre o cursor e o tubo, não temos nenhuma força na direção radial:
E na direção tangencial temos a força de contato exercida pelas paredes do tubo para carregar o cursor consigo:
Passo 2
Como nosso objetivo é calcular a força , vamos olhar primeiro para a segunda equação:
Mas como a velocidade angular é constante, temos , e então:
E conhecemos todos esses termos, exceto a velocidade radial , precisamos encontrá-la usando a outra equação.
Passo 3
Olhando para a primeira equação:
Como podemos reescrevê-la de forma que o apareça? Vamos usar a regra da cadeia:
E então a nossa equação fica da seguinte forma:
E queremos saber qual é o valor final de quando vai de até , e com :
E agora podemos substituir na equação de cima:
Pronto!
Resposta
O módulo da força exercida pelo tubo é .