Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 83
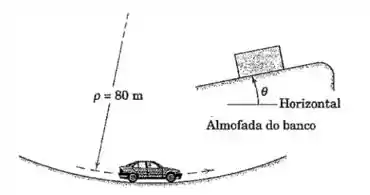
O carro tem uma velocidade de na base da depressão quando o piloto aciona os freios, provocando uma desaceleração de . Qual é o ângulo mínimo da almofada do banco para o qual um pacote não deslizará para frente? O coeficiente de atrito estático entre o pacote e a almofada do banco é (a) e (b) .
Passo 1
Vamos definir duas direções e no desenho da almofada:
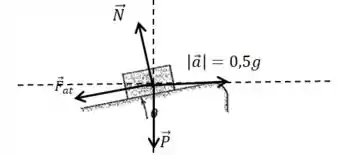
E podemos montar as equações sem problemas:
Já que tem que existir uma força centrípeta apontando para cima (centro da trajetória nesse caso).
E podemos considerar que a aceleração gera uma força que tem módulo :
Lembrando que, como nos exercícios de plano inclinado:
Passo 2
E então ficamos com o seguinte sistema:
Da primeira equação podemos encontrar o seguinte:
E podemos substituir isso na segunda:
E dividindo tudo por :
E substituind os valores numéricos:
Passo 3
Como queremos calcular o ângulo de não-deslizamento para diferentes valores de , vamos reorganizar essa fórmula:
E agora podemos calcular os dois ângulos:
(a)
(b)
Nesse segundo caso (ângulo negativo), a inclinação do banco é voltada para baixo.
Resposta
(a) e (b) .