Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 143
Determine as reações nos apoios da viga para o carregamento mostrado na figura.
Passo 1
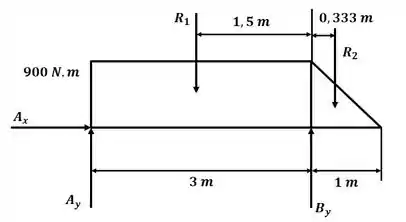
Pra começar podemos dividir o carregamento em duas regiões, uma retangular e outra triangular e calcular as resultantes em cada uma delas, então, conforme a figura a seguir, temos:
Passo 2
Agora podemos aplicar o somatório de forças na direção para obter o valor da reação em :
Agora, aplicando o somatório de momento com relação ao ponto podemos descobrir o valor da reação na direção no ponto :
Isolando e resolvendo, temos:
Passo 3
E, pra terminar, vamos aplicar o somatório de forças na direção para encontrar o valor da reação em :
Isolando e substituindo o valor de encontrado no passo 2, temos:
Resposta
Exercícios de Livros Relacionados
Determine os diagramas de esforço cortante e de momento fletor para a viga.
O eixo está apoiado por um mancal axial liso em A e um mancal radial liso em B . Determine os diagramas de esforço cortante e de momento fletor para o eixo.
Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine os diagramas de esforço cortante e de momento fletor para a viga composta.
Determine os diagramas de esforço cortante e de momento fletor para a viga.