Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 122
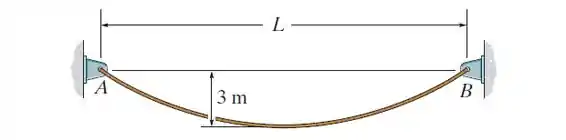
O cabo de é suspenso entre os suportes A e B. Se o cabo pode sustentar uma tração máxima de 1,5 kN e a fecha máxima é 3 m, determine a distância máxima entre os suportes.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão semelhante ao exercício resolvido 7.13. Inclusive, vamos aproveitar as equações lá desenvolvidas para resolver a questão!
Aqui o nosso objetivo é determinar a distância máxima entre os suportes. Para isto, vamos começar pela equação da flecha do cabo, a equação . Do Exemplo 7.13 nós temos que:
Antes de substituirmos os valores, vamos calcular o peso do fio! Ele será:
Continuando, vamos substituir todos os valores que a questão nos deu. Desta forma, temos:
Eita! Acabou que temos duas incógnitas na equação acima e ainda não conseguimos determinar nada!
Mas calma! Basta obtermos outra equação com ambas as incógnitas para montar um sistema e assim conseguir obter as incógnitas.
Passo 2
E agora, qual é a nossa segunda equação???
Vamos trabalhar com a tração máxima do cabo, que é e nós conhecemos. Para calcularmos a tração máxima, temos:
Só que para chegarmos na relação de , vamos ter que escrever primeiro quem é , pois esta é a única relação que nós conhecemos. Como o ângulo de máxima inclinação ocorre na extremidade A ou B do cabo, a relação será:
Mas o comprimento não importa nesta questão, apenas o comprimento , pois é ele quem escrevemos o comprimento . Então, como , temos:
E como chegamos ao cosseno? Para isto, temos a seguinte relação trigonométrica:
Agora sim chegamos a nossa segunda equação do sistema:
Passo 3
Após os dois primeiros Passos chegamos ao seguinte sistema de equação:
Resolvendo o sistema acima obtemos !
E assim finalizamos a questão!