Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 169
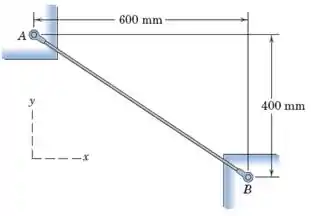
Um cabo esticado entre o suporte fixo está sob uma tensão trativa de Expresse a tensão como um vetor usando, os vetores unitários primeiro, e como uma força atuando em e como uma força atuando em
Passo 1
E aí meus queridxs, tudo bem com vocês?
Pois bem, queremos escrever nossa força trativa de forma vetorial em função e . Para isso, vamos o vamos que podemos escrever nossa força de forma vetorial utilizando o módulo do nosso vetor vezes o vetor unitário na direção que desejamos, matematicamente estamos falando de
Para o nosso problema vamos adotar o ponto como origem do nosso sistema e, assim, teremos como coordenadas para os pontos o seguinte
Passo 2
Sendo assim, nosso vetor unitário na direção será dado por
Dessa forma, vamos ter como representação vetorial para nossa força trativa o seguinte veotr
Perceba que essa força é a força de tração no ponto e essa força é o negativo da nossa força de tração no ponto . Portanto, teremos
Pronto, tá resolvido nosso problema.
