Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 124
A viga , de aço, foi projetada como uma coluna para suportar as duas forças verticais, como mostrado. Substitua essas forças por uma força equivalente simples ao longo da linha de centro vertical da coluna e um binário .
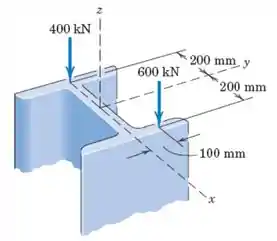
Passo 1
E aí meus queridos, tudo bom?
Então, prestem muita atenção nesse problema porque ele envolve uns detalhezinhos que podem deixar a gente confuso de não prestar bastante atenção. O problema se torna fácil, pois conseguimos encontrar as distâncias em relação ao ponto de referência de forma bem simples, claro que para a força de teremos uma parte na direção e uma parte na direção visto que ela não está alinhada com nenhum eixo. Entendido?
Passo 2
Adotando que o sentido de onde surgirá o momento é dado pela regra da mão direita vamos ter o seguinte
Pronto, temos o binário exigido pelo problema e está finalizado o nosso exercício.
