Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 13

Três cabos são unidos no anel de junção . Determine as tensões nos cabos e causadas pelo peso do cilindro de .

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para encontrar as tensões nos cabos e devido ao cilindro de massa igual a sustentado pelo cabo em D. O peso do cilindro é dado por:

Vamos analisar primeiramente o diagrama de corpo livre do cilindro isolado, com o seu peso e a tensão do cabo atuando nele:

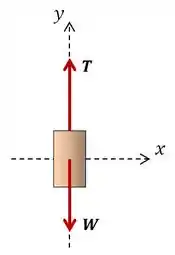
Fazendo o somatório de forças na direção do eixo , podemos descobrir a tensão deste cabo:

Onde as forças são positivas quando estão no sentido positivo de :

Bem simples né? Vamos continuar então!

Passo 2

Show, feito isso, vamos isolar o anel C com as tensões dos três cabos , e atuando nele:

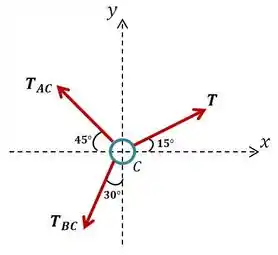
Neste caso, nós já temos o valor de , enquanto e são incógnitas que podem ser encontradas utilizando as equações de equilíbrio. Novamente vamos considerar que as forças são positivas quando estão no sentido positivo dos eixos e .