Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 112
A tensão no suporte do cabo . Escreva a força que este cabo exerce sobre a longarina como um vetor . Determine os ângulos z que a linha de ação de formam com os eixos positivos .
Passo 1
E aí meus queridos, tudo bom?
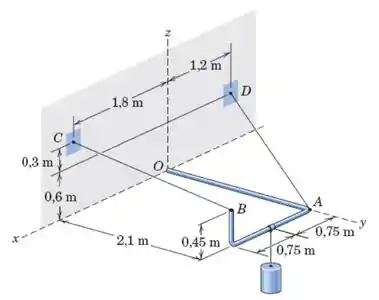
Então, prestem muita atenção nesse problema porque ele envolve uns detalhezinhos que podem deixar a gente confuso de não prestar bastante atenção. Primeiramente vamos escrever as coordenadas dos nossos pontos que são dadas por
Com isso, conseguimos escrever o vetor dado por
Dividindo esse vetor por seu módulo vamos encontrar o vetor unitário na direção que será dado por
Passo 2
Dessa forma, nossa força pode ser escrita como sendo
Passo 3
Agora, podemos calcular os ângulos que o vetor forma com cada um dos eixos usando a seguinte fórmula
Que é uma consequência da definição do produto escalar. Agora, vamos aplicar essa fórmula a cada uma das componentes de modo a obter
Agora é só calcular os ângulos usando a calculadora
Pronto, tá resolvido nosso problema.