Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 26
O cabo evita que a barra gire no sentido horário em torno do pivô . Se a força trativa no cabo vale , determine os componentes e desta força, atuando no ponto da barra.
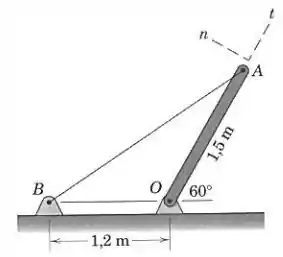
Passo 1
Pessoal, vamos representar a tração no cabo e suas componentes e na figura a seguir:
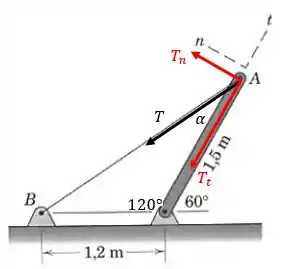
Primeiramente, vamos utilizar a lei dos cossenos para calcular o comprimento , informação que será necessária mais tarde:
Passo 2
Show! Agora podemos calcular o ângulo entre a tração e o eixo , por meio da lei dos senos:
Logo,
Resposta
Exercícios de Livros Relacionados
Uma estaca é puxada do solo por meio de duas cordas como mostra a figura. Sabendo que a intensidade, direção e sentido da força exercida em uma das cordas, determine a intensidade, a direção e o senti
A direção e o sentido das forças de 330 N podem variar, mas o ângulo entre elas é sempre 50°. Determine o valor de α para que a resultante das forças atuantes em A seja na horizontal e para a esquerda
O elemento BD exerce sobre o elemento ABC uma força P dirigida ao longo da linha BD. Sabendo que P deve ter um componente vertical de 1068 N, determine ( a ) a intensidade da força P, ( b ) sua compon
Dois cabos estão ligados juntos em C e carregados como mostra a figura. Sabendo que P = 360 N, determine a tensão a no cabo AC, ( b ) no cabo BC.
Determine a intensidade da força resultante que atua sobre a chapa e sua direção, medida no sentido anti-horário a partir do eixo x positivo.