Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 29

Um cabo homogêneo de comprimento L e seção transversal uniforme é suspenso por uma das extremidades. (a) designado por p a densidade (massa por unidade de volume) do cabo e por E seu modulo de elasticidade, determine a deformação do cabo em razão de seu próprio peso. (b) mostre que a mesma deformação seria obtida se o cabo estivesse na horizontal e se uma força igual à metade de seu peso fosse aplicada a cada extremidade.

Passo 1

Fala aí gurizada tudo belezinha, antes de tudo vamos esboçar o diagrama de corpo livre para facilitar os cálculos, então vem comigo :D

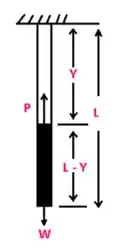
Para o elemento no ponto identificado pela coordenada y.

P= peso da porção abaixo do ponto.

= p g A L - y d δ = P d y E A = p g A L - y E d y = p g E L y - 1 2 y 2 L 0

= p g E L 2 - L 2 2

Peso total: W = p g A L F = E A δ L = E A L   x   1 2 p g L E = 1 2 p g A L

  1. Isolando δ   temos:

    2. δ = 1 2 p g L 2 E

  2. F = 1 2 p g A L = 1 2 W

Resposta

  1. δ = 1 2 p g L 2 E
  2. F = 1 2 W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado plano de tensões mostrados, determinar:Os planos principais As tensões principaisA máxima tensão de cisalhamento.
Para a barra do P r o b . 6.150 , e sabendo-se que o aço usado E = 200G P a e ϑ = 0,30 , determinar as três deformações especificas principais e a máxima deformação especifica de cisalhamento, no pont
As fibras de uma peça de madeira formam um ângulo de 15° com a vertical. Para o estado plano de tensões mostrado, determinar:A tensão de cisalhamento, no plano, paralelo as fibras;A tensão normal perp
um extensômetro é colado horizontalmente, numa superfície cilíndrica de um vaso de pressão de 600m m de diâmetro externo e 7,50 m m de espessura da parede. Sabendo-se que E = 200G P a e ϑ = 0,25 e que
Um vaso de pressão esférico é fabricado com chapa de aço de 100mm de espessura e com tensão última igual a 360M p a . Sabendo-se que uma pressão máxima admissível de 4,5M P a é desejada, e que um coef