Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 52

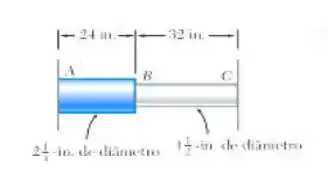
Uma barra formada por duas partes cilíndricas AB e BC está impedida de se deslocar em ambas as extremidades. A parte AB é feita de latão ( E l a t a o = 29   x   10 6 p s i ,   a l a t ã o = 6,5   x   10 - 6 / ° F ) e a parte BC é feita de aço ( E a ç o = 10,4   x   10 6 p s i ,   a a ç o = 13,3   x   10 - 6 / ° F ) . Sabendo que a barra está inicialmente livre de tensões, determine (a) as tensões normais nas partes AB e BC provocadas por um aumento de 70°C na temperatura e (b) o deslocamento correspondente do ponto B.

Passo 1

Fala aí galera tudo belezinha? Para calcularmos as tensões normais primeiramente vamos desenhar o diagrama de corpo livre e depois partiu determinar a área das seções 0/

Agora simm , a área :D

A A B = π 4 2.25 2 = 3,9761   i n ²           A B C = π 4 1.5 2 = 1,76715   i n ²  

Sabendo que a expansão térmica é de: ∆ T = 70 ° F , temos os seguintes alongamento respectivos as áreas estudadas:

( δ T ) A B = L A B α s ∆ T = 24   x   6,5   x   10 - 6   x   70 = 10,92   x   10 - 3 i n . ( δ T ) B C = L B C α a ∆ T = 32   x   13,3   x   10 - 6   x   70 = 29,792   x   10 - 3 i n .

Total: δ T = ( δ T ) A B + ( δ T ) B C = 40,712   x   10 - 3 i n .

E devido à força compressiva induzida por P temos:

( δ P ) A B = P L A B E s A A B = 24 P 29   x   10 6   x   3,9761 = 208,14   x   10 - 9 P ( δ P ) B C = P L B C E a A B C = 32 P 10,4   x   10 6   x   1,76715 = 1741,18   x   10 - 9 P

Total: δ P = ( δ P ) A B + ( δ P ) B C = 1949,32   x   10 - 9 P

Para a deflexão consideramos que:

δ P = δ T

1949,32   x   10 - 9 P = 40,712   x   10 - 3

Passo 2

Agora sim gurizada podemos determinar as tensões normais nas partes AB e BC provocadas por um aumento de 70°C e o deslocamento

  1. σ A B = - P A A B = - 20,885   x   10 3 3,9761 = - 5,25   x   10 3 p s i σ B C = - P A B C = - 20,885   x   10 3 1,76715 = - 11,82   x   10 3 p s i

  2. ( δ P ) A B = 208,14   x   10 - 9   x   20,885   x   10 3 = 4,3470   x   10 - 3 i n . δ B = ( δ T ) A B → + ( δ P ) A B ← = 10,92   x   10 - 3 → + 4,3470   x   10 - 3 ←

Ou,

( δ P ) B C = 1741,18   x   10 - 9   x   20,885   x   10 3 = 36,365   x   10 - 3 i n . δ B = ( δ T ) B C ← + ( δ P ) B C → = 29,792   x   10 - 3 ← + 36,365   x   10 - 3 →   = 6,57   x   10 - 3 i n . →

Resposta

  1. σ A B = - 5,25   k s i e σ B C = - 11,82   k s i
  2. δ B = 6,57   x   10 - 3 i n . →
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada barra de treliça mostrada na figura tem uma seção transversal uniforme de área A . Usando o método do trabalho e da energia, determine o deslocamento horizontal do ponto de aplicação da força P .
As barras de treliça mostradas na figura são feitas de aço e têm as áreas das seções transversais mostradas na figura. Usando E = 200G P a , determine o deslocamento vertical do nó C provocado pela ap
Levando em conta apenas o efeito das tensões normais, determine a energia de deformação da viga prismática AB para o carregamento mostrado.
Levando em conta apenas o efeito das tensões normais, determine a energia de deformação da viga prismática AB para o carregamento mostrado.
E = 10,5 × 10 6 p s i . Determine a energia de deformação da treliça para o carregamento mostrado.