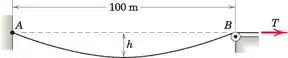
Um cabo que pesa 50 newtons por metro de comprimento é preso no ponto A e passa sobre a polia pequena em B no mesmo nível sob uma tensão T. Determine o valor mínimo de T para suportar o cabo e a deflexão h correspondente.
Passo 1
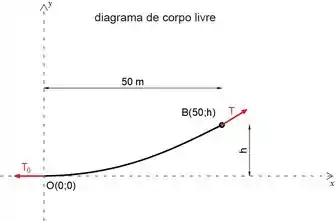
Primeiro, vamos desenhar o diagrama de corpo livre do cabo.
Observe que cortamos o cabo pouco antes de ele atingir a polia a B.
Uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária
Como os pontos A e B estão na mesma altura, o ponto mais baixo do cabo (início do sistema de coordenadas) está no meio.
Passo 2
Para determinar o valor mínimo da tensão T, precisaremos escrever sua função e encontrar sua primeira derivada (já que a primeira derivada é igual a zero no mínimo e no máximo de uma função).
Substitua por seu valor ex pela coordenada do ponto B, uma vez que a tensão T atua no ponto B.
Observe que a tensão T é função de T0, portanto, derivaremos a expressão acima em relação a T0.
Passo 3
Usando uma calculadora de derivativos passo a passo como derivative-calculator.net, derivaremos a expressão acima.
Como dissemos antes, para determinar o valor mínimo da função T(T0), precisaremos igualar a primeira derivada, ou seja, a expressão (2) a zero.
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente a expressão (2) e ler o valor de T0 em T(T0) = 0
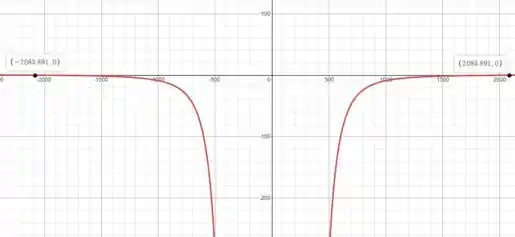
Observe que existem duas soluções:
Uma solução indica que a função T(T0) é máxima naquele ponto e a outra que a função é mínima.
Passo 4
Existem algumas maneiras de verificar se a função está em seu máximo ou mínimo em um determinado ponto, mas a mais fácil é desenhar a função. Mais uma vez usando uma calculadora gráfica como o Desmos, podemos ver que a função T(T0) é mínima em:
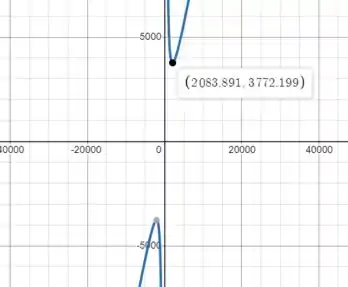
Substitua T0 por seu valor na expressão (1) para determinar a tensão mínima T necessária para manter o cabo na posição
Passo 5
Observe que, uma vez que o cabo torce uma forma catenária, sua função é:
Substitua T0 e por seus valores e coloque as coordenadas do ponto B na equação.
Finalmente, a curvatura h é: