Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 166
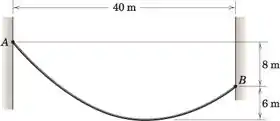
Encontre o comprimento total L do cabo que terá a configuração mostrada quando suspenso nos pontos A e B.
Passo 1
Primeiro, vamos desenhar o diagrama de corpo livre do cabo. Observe que o início do sistema de coordenadas está no ponto mais baixo do cabo, que está posicionado na distância l à esquerda do ponto B.
A partir do esboço abaixo, podemos ver que as coordenadas dos pontos A e B são:
e
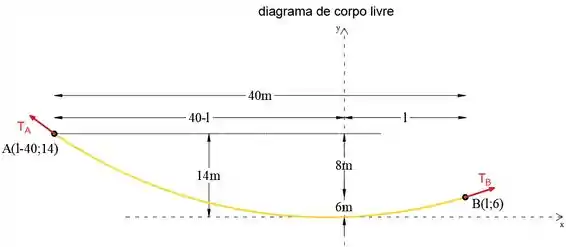
Passo 2
Usando a expressão (5/20), podemos escrever o comprimento do cabo do início da coordenada ao ponto A e ao ponto B como:
E o comprimento total do cabo é igual à soma dessas duas partes.
Passo 3
Observe que na equação (1) a razão T0/ é desconhecida, que podemos determinar a partir da expressão (5/19)
Coloque as coordenadas do ponto A na equação
Coloque as coordenadas do ponto A na equação
Passo 4
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente as funções (A) e (B) e ler o valor de e l que satisfaz ambas as equações do ponto de intersecção
Observe que você precisará ampliar o gráfico para poder ler as coordenadas do ponto de intersecção
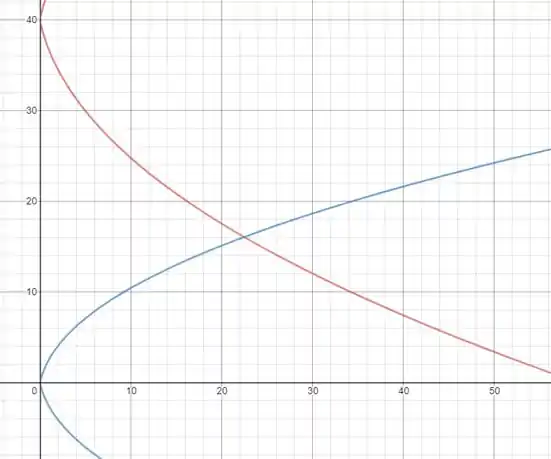
Finalmente, vamos substituir por seu valor na equação (1)
Passo 5
Vamos transferir isso para
Um dito na etapa 2, se refere à massa do cabo mais a massa do gelo por metro, então a massa do gelo por metro é
Substitua e por seus valores
Finalmente, obtemos que a massa máxima por metro de gelo que o cabo pode suportar é