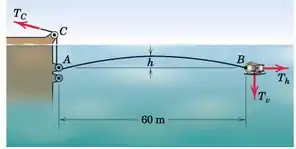
Um pequeno veículo robótico subaquático controlado remotamente e sua corrente são posicionados conforme mostrado. O veículo com flutuação neutra possui propulsores independentes para controle horizontal e vertical. A corda, projetada para ser ligeiramente flutuante, tem uma força líquida para cima de 0,025 N por metro de seu comprimento agindo sobre ela. Existem 60,5 m de cabo entre os pontos A e B. Determine as forças horizontais e verticais que o veículo deve exercer sobre o cabo em B para manter a configuração mostrada. Além disso, encontre a distância h. Suponha que a corda entre os pontos A e B esteja totalmente submersa.

A seguir, como o cabo suporta apenas seu peso, o cabo tem um formato conhecido como catenária, portanto, para determinar a altura h, usaremos a expressão (5/19)

Coloque as coordenadas do ponto B na equação

Observe que T0 e m são desconhecidos, bem como a razão T0/, que podemos determinar a partir da expressão (5/20)

Substitua x pela coordenada do ponto B e s por seu valor

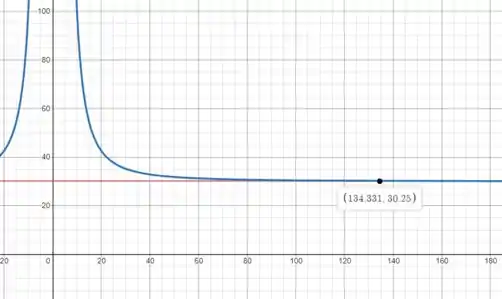
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função e leremos o valor de em

A partir daqui, podemos expressar como

Vamos agora substituir por seu valor na equação (1)

Percebemos que a altura h é

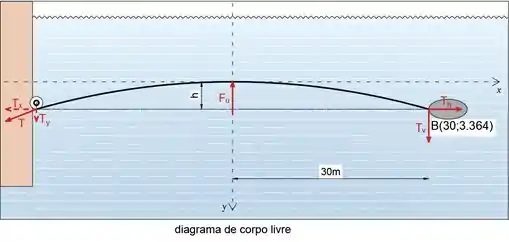
A fim de determinar as forças que o veículo exerce, precisaremos desenhar o diagrama de corpo livre

A força líquida para cima é igual a

Usando simetria, conhecemos as seguintes relações:

Portanto, podemos escrever expressões para a tensão T como

Ao igualar a soma das forças nas direções y a zero, podemos determinar a força Tv

Substitua Ty por Tv e Fu por seu valor

Uma vez que a força Th é na verdade o componente x da tensão do cabo, conforme mostrado na 6ª etapa, o seguinte se aplica:

Usando a expressão (5/22), podemos determinar a força Th

Substitua T por , por e y pela coordenada do ponto

Em seguida, substitua T0 por Th e Tv por seu valor

Quadrado ambos os lados da equação

A partir daqui, podemos expressar Th como