Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 172
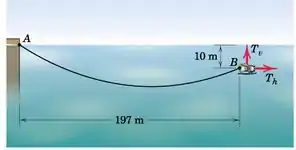
O veículo robótico controlado remotamente do Prob. 5/171 está agora conectado a uma corda de 200 m que tem uma ligeira flutuabilidade negativa em que uma força descendente líquida de 0,025 N por metro de seu comprimento atua sobre ela. Determine os componentes horizontal e vertical de empuxo que devem ser produzidos para manter o veículo na posição mostrada. O próprio veículo tem flutuabilidade neutra.
Passo 1
No esboço abaixo, podemos ver que as coordenadas dos pontos A e B são
e
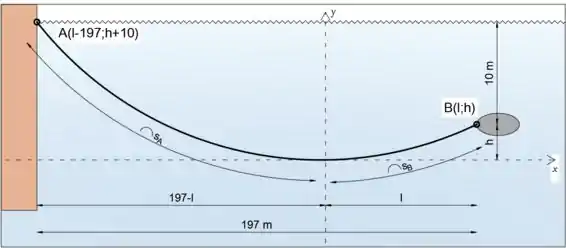
Vamos escrever a expressão para o comprimento do cabo (5/20)
Coloque a coordenada x dos pontos A e B na expressão acima para determinar os comprimentos sA e sB
Portanto, o comprimento total do cabo é
Sabemos que o cabo tem 200 m de comprimento, então podemos substituir sA + sB por 200
Passo 2
A seguir, vamos escrever a expressão para coordenada y do cabo (5/19)
Coloque as coordenadas do ponto A na equação
Coloque as coordenadas do ponto B na equação
Vamos subtrair yB de yA para obter a diferença de altura entre os pontos
Passo 3
Vemos pelo desenho que a diferença de altura entre os pontos é de 10 m, então podemos substituir yA yB por 10
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente as funções (1) e (2) e ler os valores de e l que satisfaz ambas as equações do ponto de intersecção
Observe que você precisará ampliar o gráfico para poder ler as coordenadas do ponto de intersecção
Passo 4
A partir daqui, podemos expressar como
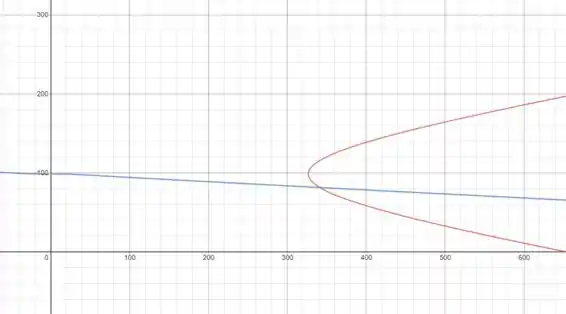
Agora, podemos determinar a coordenada yB (altura h), colocando os valores calculados na expressão escrita na etapa 3
Observe que a coordenada y do ponto A é
A fim de determinar as forças que o veículo exerce, precisaremos desenhar o diagrama de corpo livre
A força descendente líquida é igual a
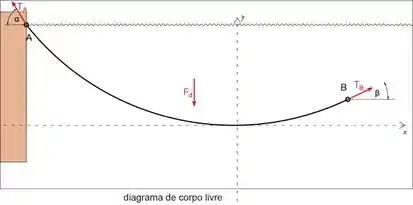
Passo 5
Usando a expressão (5/22), determinaremos as tensões em A e B
Substituir por
E coloque as coordenadas y do ponto A (B) na equação
Sabemos que T0 é na verdade o componente x da tensão através do cabo, então podemos escrever como
A partir daqui, podemos escrever a expressão para e
Passo 6
Equacionando a soma das forças na direção y a zero, podemos determinar a torção T0
Substitua TA por 1.0580T0, TB por 1.0286T0 e ângulos por seus valores
A partir da expressão escrita na 7ª etapa, determinaremos que a tensão do cabo em B é
Finalmente, vamos isolar e desenhar o diagrama de corpo livre do veículo
Equacionando a soma das forças na direção x, determinaremos a força Th
Equacionando a soma das forças na direção y, determinamos a força T,