Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 160
Repita Prob. 5/159, mas não use a aproximação de um cabo parabólico. Compare seus resultados com as respostas impressas para Prob. 5/159.
Passo 1
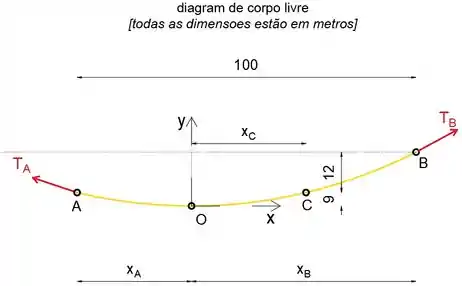
Vamos desenhar o diagrama de corpo livre do cabo.
Podemos ver que as coordenadas dos pontos A e B são:
Também podemos ver que a distância horizontal entre A e B é:
E o peso do cabo por unidade de comprimento é:
Observe que os pontos A e C estão na mesma altura, portanto as distâncias horizontais xA e xc são iguais.
Sabendo disso, podemos escrever a distância horizontal entre os pontos A e C como:
Passo 2
Como o cabo é catenária, sua função é:
Substitua por seu valor para obter:
Podemos determinar a componente vertical da tensão no cabo (T0) colocando as coordenadas dos pontos A e B na expressão (3).
Ponto A:
Ponto B:
Some as equações (A) e (B) para obter:
Passo 3
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente as funções (A.1) e (B.1) e ler o valor de T0 a partir do ponto de intersecção
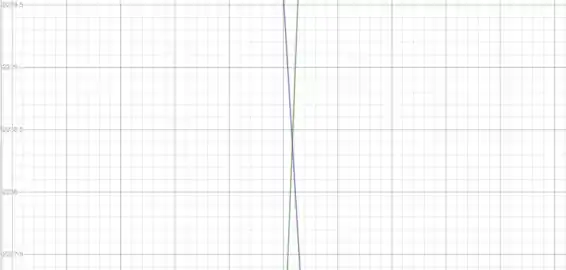
Colocando o valor de T0 na expressão (A), podemos determinar xA.
Multiplique os dois lados da equação por
A partir daqui, podemos expressar xA como:
Finalmente, substitua xA por seu valor na equação (2)
Passo 4
Usando a expressão (5-22), podemos calcular a tensão no ponto B.
Finalmente, iremos isolar e desenhar o diagrama de corpo livre do cilindro.
Observe que a tensão no cabo preso ao cilindro é igual à tensão no cabo no ponto B por causa da polia.
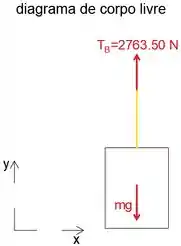
Equacionando a soma das forças na direção y a zero, podemos determinar a massa m
Passo 5
Em comparação com os resultados aproximados do problema anterior, podemos concluir que tanto m quanto a distância X|AC| são maiores.